Wastewater Treatment Plant Design...

Chapter 06 - Sludge Treatment and Disposal...

Nomenclature...

Symbol Definition Units
MC Moisture content. Mass of liquid in sludge / mass of sludge %
SC Solids content. Mass of solids ( dry mass ) in sludge / mass of sludge %
V Volume of sludge or filtrate m 3
M S Mass of dry solids in sludge kg
M W Mass of liquid in sludge kg
VM Volatile matter ( = organic content ) %
TS Total solids kg
X Volume of digester gas used in boiler m 3
r Specific resistance to dewaterability m / kg
C Solids concentrations in sludge kg / m 3
THETA Filtration time s
MU Absolute viscosity of filtrate N . s / m 2
P Pressure ( difference ) across filter N / m 2
A Filter area m 2
R M Resistance of filter paper, cloth or septum 1 / m
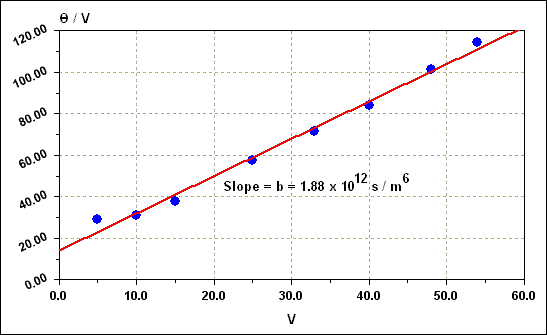
b Slope of THETA / V versus V plot s / m 6
r O Specific resistance constant -
S Coefficient of compressibility Dimensionless
C T Mass of solids / unit volume of liquid in the sludge kg / m 3
Y Yield of vacuum filter kg / m 2 . s
A F Area of cake formation as fraction of total area -
THETAR Time of l revolution s
f E Cake correction factor, ratio mass of liquid / unit mass sludge : mass of filtrate / unit mass sludge dewatered -
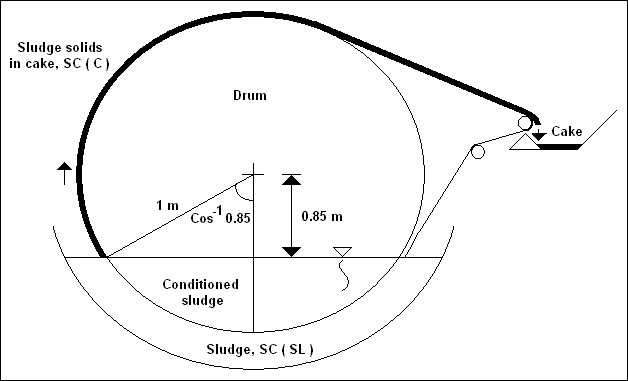
SC ( Sl ) Solids content of wet sludge Fraction
SC ( C ) Solids content of sludge as it emerges from the filter bath Fraction
T Time of pressure filtration h
k Constant of proportionality, emprical kg 2 / m 2 . s for T in s
SC ( F ) Final cake solids content at end of filter pressing Fraction
H Heat energy required to raise water to incinerator exit temperature J
T L Inlet temperature of sludge O C
T E Exit temperature of exhaust gases O C
K Calorific value or energy / volume of combustible material J / kg
CM Combustible material ( almost equivalent to organic material ) -
Z Fraction of calorific value taken up by incinerator heat loss -

6.1. Sludge Volume and Moisture Content...

The magnitude of the problem is indicated by the simple calculation that, if a city of 1 million people produces waste sludge at 0.09 kg / capita . day at 97 % moisture content, the city faced with the daily disposal of 3,000 m 3 of sludge. Sludges produced in wastewater treatment typically contain very small amounts of solids distributed throughout a large volume of liquid. The moisture content ( MC ) is expressed as ;

MC = ( Mass of liquid in the sludge / Mass of sludge ) ( 100 % )

and the solids content SC = 100 - MC. At high MC values, the volume V 2 produced by dewatering a volume of sludge V 1 , from MC 1 to MC 2 is given by approximation ;

V 2 = ( V 1 ) [ ( 100 - MC 1 ) / ( 100 - MC 2 ) ] = ( V 1 ) ( SC 1 / SC 2 )

Example 6-1 :

A sludge of 99.5 % MC containing 5 kg dry SS is dewatered progressively to 99, 97, 90 and 70 % MC. Calculate the change in volume at each MC using equation given above. Assuming that dry sludge solids and water have densities of 1,400 and 1,000 kg / m 3 , respectively, estimate the error produced in the calculation of sludge volume at 70 % MC by using the approximate equation.

Calculation :

At 99.5 % MC 5 kg dry SS are associated with 1,000 kg sludge. The volume is ;

V = ( 5 / 1,400 ) + ( 1,000 - 5 ) / ( 1,000 ) = 0.999 m 3 = 1 m 3 sludge

at MC 99 % : V 2 = ( 1 ) [ ( 100 - 99.5 ) / ( 100 - 99 ) ] = 0.500 m 3
at MC 97 % : V 2 = ( 1 ) [ ( 100 - 99.5 ) / ( 100 - 97 ) ] = 0.167 m 3
at MC 90 % : V 2 = ( 1 ) [ ( 100 - 99.5 ) / ( 100 - 90 ) ] = 0.050 m 3
at MC 70 % : V 2 = ( 1 ) [ ( 100 - 99.5 ) / ( 100 - 70 ) ] = 0.0167 m 3

Using a density approach, at 99 % MC 5 kg dry SS is associated with 500 kg sludge or 495 kg water. Thus the volume is ;

V 99 % = ( 5 / 1,400 ) + ( 495 / 1,000 ) = 0.499 m 3

The volumes are similarly 97 % MC ; 0.165 m 3 ; 90 % MC ; 0.0486 m 3 ; 70 % MC ; 0.0152 m 3 . Assuming the density calculations to be correct, the sludge volume at 70 % MC using equation given above is approximately 10 % greater than the correct volume.

6.2. Liquor Production From Treatment Processes...

A simple way of calculating the liquor produced from particular treatment processes is sometimes useful and can be estimated as follows. Since the solids content ;

SC ( % ) = [ ( M S ) / ( M S + M W ) ] ( 100 % )

where ; M S and M W are the mass of solids and water, respectively, in the sludge, then ;

( 100 - SC ) ( M S ) = ( SC ) ( M W )

or, considering 1 kg of solids ;

( 100 / SC ) - 1 = M W

For most calculations M W ( kg ) x 10 - 3 gives the associated liquor volume in m 3 . The liquor released in a process which dewaters sludge from SC ( 1 ), %, to SC ( 2 ), %, is therefore ;

Liquor volume = ( 1 / 10 ) [ ( 1 / SC - 1 ) - ( 1 / SC - 2 ) ] ( M S ) ( m 3 )

Example 6-2 :

A sludge which is initally at 6 % SC is dewatered in a filter press to 40 % SC. Calculate the liquor produced in pressing 100 kg dry sludge solids.

Calculation :

At 6 % SC, 1 kg solids is associated with ;

( 100 / 6 ) - 1 = 15.7 kg water

at 40 % SC, 1 kg solids is associated with ;

( 100 / 40 ) - 1 = 1.5 kg water

Therefore, pressing 100 kg sludge would produce ;

[ ( 100 ) ( 15.7 - 1.5 ) ] / ( 1.00 ) = 1.42 m 3 liquor

6.3. Anaerobic Digestion...

The characteristics of wastewater sludges, and more particularly primary settlement sludges, which most severely limit the methods that may be used for their disposal, are their smell and unaesthetic appearance. Aerobic oxidation is not usually used for other than secondary activated sludges, however, if other sludges are kept anaerobic, they will break down to produce a tarry smelling, blackish, relatively innoccuous material. The anaerobic digestion of sludges may be carried out at cryophilic ( 10 - 15 O C ), mesophilic ( 30 - 34 O C ) or thermophilic ( 50 - 55 O C ) temperatures. The mesophilic process is often used to produce a less obnoxious sludge and a combustible gas mixture ( 66 % CH 4 and 34 % CO 2 ). The process is often carried out in a heated, partially mixed anaerobic primary digester of the type shown in figure below with a secondary dewatering tank being used prior to drying beds or final sludge disposal.



1 : Sludge return pipe from heating system
2 : Bottom draw - off pipe
3 : Secondary draw - off pipe
4 : Main draw - off pipe
5 : Gas collection dome
6 : Roof stop
7 : Effluent weir
8 : Sludge feed pipe to heating system

Typical primary digester dimensions are given in table shown below.

Nominal capacity ( m 3 ) A ( m ) B ( m ) C ( m ) D ( m ) E ( m ) F ( m ) Size of screw pump ( m )
710 10.7 0.69 7.9 5.6 5.2 1.07 0.30
990 12.2 0.76 8.5 6.0 5.2 1.22 0.46
1,420 13.7 0.91 9.5 6.9 5.5 1.22 0.46
1,840 15.2 0.99 10.0 7.2 6.1 1.37 0.61
2,410 16.8 1.07 10.8 8.1 6.7 1.37 0.61
3,540 18.3 1.22 13.3 10.5 6.7 1.52 0.61
4,250 19.8 1.30 13.6 10.4 6.7 1.83 0.61

General working parameters which have been found useful in practice for primary digesters are given in table show below.

Volatile solids loading ( kg VM / m 3 . day ) 1 - 2
Solids loading ( kg SS / m 3 . day ) 1.5 - 2.1
Input sludge slolids ( SC % ) 2 - 6
Total solids destruction ( TS input % ) 30 - 35
Input sludge VM ( VM as total solids % ) 70 - 80
Volatile matter ( VM ) destruction ( VM input % ) 40 - 46
Gas production ( m 3 / kg VM destroyed ) 0.9 - 1.2
Sludge gas calorific value ( kJ / m 3 ) 22,400

6.3.1. General Relationships...

The data given in table shown above may be used to assess retention times, per capita digestion capacity, per capita gas production etc.

Example 6-3 :

Assuming sludge production is 0.080 kg dry SS / capita . day at 9 % MC, calculate the nominal retention time in a mesophilic digester using solid and volatile solids loadings from table shown above.

Calculation :

Using a VM loading of 1.5 kg VM / m 3 . day at 75 % VM this is equivalent to ;

[ ( 0.090 ) ( 0.75 ) ] / ( 1.5 ) = 0.045 m 3 / capita

The volume of sludge produced per capita day at an average input SC of 4 % ( 40 kg / m 3 ) is ;

0.090 / 40 = 2.25 x 10 - 3 m 3

The nominal retention time is therefore ;

0.045 / 2.25 x 10 - 3 = 20 days

Using a dry SS loading of 1.8 kg / m 3 . day gives a per capita volume of 0.09 / 1.8 = 0.05 m 3 and a retention time of 0.05 / 2.25 x 10 - 3 = 22 days

Gas production can similarly be estimated.

Example 6-4 :

Determine the gas production per head of population and determine the maximum energy available given a sludge gas calorific value of 22,400 kJ / m 3 .

Calculation :

Assume 0.085 kg dry SS / capita . day at 75 % VM with 43 % VM reduction. The organics destroyed total ;

( 0.085 ) ( 0.75 ) ( 0.43 ) = 0.027 kg / capita . day

At 1.1 m 3 gas / kg VM destroyed, the gas volume produced is 0.030 m 3 gas / capita . day, i.e.

( 22,400 ) ( 0.030 ) = 672 kJ / capita . day

6.3.2. Heat Budget Calculations...

There are two major heat requirements in anaerobic digestion which must be satisfied if the digester is to remain at the operational temperature. They are the heat ;

( a ) to raise the daily sludge input volume to the operating temperature,
( b ) to keep the whole digester volume at the operating temperature.

This latter heat requirement can be calculated. However, it is more common to estimate it in terms of " equivalent drop in temperature in digester contents " over a day. This is usually estimated from experience and is often more accurate than lengthy calculations of heat transmittance through walls, roofs, etc. There is a gain in heat from the gas.

Example 6-5 :

Calculate the heat budget for a mesophilic digester system, serving 100,000 population, producing 0.080 kg dry SS / capita . day at 97 % MC with a mean yearly temperature of 12 O C. The retention time is 25 days at 32 O C and the digester heat loss equivalent is 0.5 O C / day.

Calculation :

The daily sludge mass produced = ( 100,000 ) ( 0.080 ) = 8,000 kg dry SS / day. Since 97 % MC is 3 % SC or approximately 30 kg dry SS / m 3 sludge, the daily volume produced is 8,000 / 30 = 267 m 3 . The digester ( liquid ) volume is ( 267 ) ( 25 ) = 6,680 m 3 ( probably divided equally between two digester tanks ).

( a ) Heat Losses :

The specific heat, or specific heat capacity of sludge at 97 % is almost equal to 4.18 x 10 3 kJ / m 3 . O C. Therefore the heat loss to the surroundings at an equivalent loss of 0.5 O C / day is ;

( 4.18 x 10 3 ) ( 0.5 ) ( 6,680 ) = 14.0 x 10 6 kJ / day

The heat required to raise a daily input of 267 m 3 of sludge through ( 32 - 12 ) O C is ;

( 4.18 x 10 3 ) ( 32 - 12 ) ( 267 ) = 22.3 x 10 6 kJ / day

The total heat required per day is 36.3 x 10 6 kJ / day

( b ) Gas Production :

Assuming 30 % total solids digestion producing 1.1 m 3 gas / kg solids destroyed, the gas production is ;

( 8,000 ) ( 0.3 ) ( 1.1 ) = 2,640 m 3 gas / day

This is a theoretical heat energy of ( 2,640 ) ( 22,400 ) = 59.1 x 10 6 kJ / day. There is apparently a considerable excess of heat, i.e. 22.9 x 10 6 kJ / day.

( c ) Gas Utilization :

The gas is usually split between a boiler / heat exchanger system and a dual fuel engine. The former usually gives around 60 - 80 % efficiency as heat for the digester while the latter can give 20 - 25 % as exhaust jacket heat ( to heat the digester ) and 30 % as usable work ( driving pumps or an alternator set ). The most efficient use of the gas is one where the sum of the heats produced just equals the digester requirements.

Example 6-6 :

Given the efficiencies quoted above and the gas production from Example 6-5 calculate the most economical gas distribution between the boiler and the dual fuel engine.

Calculation :

For the 2,640 m 3 of gas produced in Example 6-5 let X m 3 go to the boiler at 70 % efficiency and ( 2,640 - X ) m 3 to the dual fuel engine at 25 % ( thermal ) efficiency, then ;

( 0.70 ) ( X ) ( 22,400 ) + ( 0.25 ) ( 2,640 - X ) ( 22,400 ) kJ

should sum to give 36.3 x 10 6 kJ. Thus X = 2,135 m 3 / day, i.e. 2,135 m 3 gas / day is used by the boiler and 505 m 3 gas / day is used by the dual fuel engine. The 505 m 3 of gas to the dual fuel engine therefore gives ( at 30 % efficiency ) ( 505 ) ( 0.30 ) ( 22,400 ) = 0.94 x 10 3 kWh / day.

6.3.3. Effect of Variables on the Heat Budget...

One of the most readily variable parameters is the input sludge solids content. Because this has a profound influence on the amount of liquid to be sustained at the operating temperature it changes the heat budget considerably.

Example 6-7 :

Assuming the values of the digestion parameters given in Example 6-5 remain the same, with the sole exception of the input sludge concentration, calculate the effect on the heat budget of input sludge consolidation to 5 % SC.

Calculation :

The daily sludge input volume changes to ( 8,000 ) / ( 50 ) = 160 m 3 / day. The heat requirements then become ;

( a ) Input sludge heat requirement = ( 14.0 x 10 6 ) ( 160 / 267 ) = 8.4 x 10 6 kJ / day
( b ) The digester heat loss to the surroundings = ( 22.3 x 10 6 ) ( 160 / 267 ) = 13.4 x 10 6 kJ / day

and the total heat requirement drops to 21.8 x 10 6 kJ / day, i.e. a reduction of 40 %.

Example 6-8 :

Assuming the conditions given originally in Example 6-5, consider the effects of reducing the retention time to 20 days ( with a corresponding lowering of solids digestion to 28 % as total solids ).

Calculation :

The input sludge rfequirement remains at 22.3 x 10 6 kJ / day ; the ambient loss reduces to ( 14.0 x 10 6 ) ( 20 / 25 ) kJ / day or 11.2 x 10 6 kJ / day, and the gas evolution becomes ;

( 2,640 ) ( 28 / 30 ) = 2,464 m 3

which is equivalent to 55.2 x 10 6 kJ / day. Overall there is a change of [ ( 55.2 - 59.1 ) + ( 14.0 - 11.1 ) ] x 10 6 kJ / day, i.e. 1.0 x 10 6 kJ / day loss of available heat energy.

6.4. Specific Resistance...

Wastewater sludges are often difficult to dewater and even spadeable sludges may still be at 75 - 80 % MC. Because the volume is critically dependent on the MC it is necessary to have some quantitative assessment of the ease with which a sludge can be dewatered. The most commonly accepted and theoretically useful concept is that of specific resistance. The specific resistance to dewatering r ( m / kg ) is related to volume of filtrate discharged V ( m 3 ) in time THETA ( s ) as ;

( THETA / V ) = { [ ( MU ) ( r ) ( C ) ] / [ ( 2 P ) ( A 2 ) ] } ( V ) + [ ( MU ) ( R M ) ] / [ ( A ) ( P ) ]

where ; M : absolute viscosity ( N . s / m 2 ), P : pressure difference over the filter ( N / m 2 or Pa ), A : filtration area ( m 2 ), R M : resistance of the filter media ( paper, cloth etc., 1 / m ) and C : sludge concentration ( kg / m 3 ). The determination of r may be carried out in an apparatus similar to that in figure given below. Plotting values of ( THETA / V ) versus V gives straight lines whose slope b is related to r as ;

r = [ ( 2 b ) ( P ) ( A 2 ) ] / [ ( MU ) ( C ) ]



- Dewatering cylinder : Base 70 mm, total length 150 mm, inlet diameter 41 mm
- Filter paper : Whatman no.1, diameter 55 mm
- Filter plate : Diameter 50 mm, hole size 1 / 16 inch
- Gauze : Fine copper mesh, diameter 41 mm

Example 6-9 :

The following set of results in table given below, were obtained from a specific resistance test carried out in the laboratory. Determine the specific resistance of the sludge.

Time ( s ) 145 310 570 1,440 2,360 3,360 4,880 6,170
Filtrate ( m 3 x 10 - 6 ) 5 10 15 25 33 40 48 54
Sludge MC = 96 %
Manometric pressure reading = 675 mm Hg
Buchner funnel diameter = 50 mm
Filtrate temperature = 20 O C

Calculation :

An MC of 96 % = 40 kg / m 3 for the solids concentration C. 675 mm Hg = ( 133.3 ) ( 675 Pa ) = 90 kN / m 2 ( kPa ). Filtration area = ( 3.14 ) ( 0.05 2 ) / ( 4 ) = 1.96 x 10 - 3 m 2 . Assuming the filtrate to be water at 20 O C, MU = 1 x 10 - 3 N . s / m 2 . Values of ( THETA / V ) versus V give the plot shown below.



Usually a few points close to the origin have to be ignored in order to obtain a straight line. In this case b = 1.88 x 10 12 s / m 6 . Therefore ;

r = [ ( 2 x 1.88 x 10 12 ) ( 90 x 10 3 ) ( 1.96 x 10 - 3 ) 2 ] / [ ( 1 x 10 - 3 ) ( 40 x 10 - 3 ) ] = 3.3 x 10 13 m / kg

6.4.1. Specific Resistance Units...

Prior to metrication, pressures were often read off gauges as g / cm 2 and thus r was quoted in units of s 2 / g. In fact the gauges indicated force / cm 2 ; thus 1 g force / cm 2 read on the gauge was 981 dynes / cm 2 . Thus " old " values of r quoted in s 2 / g require to be multiplied by 9,810 to convert them to m / kg.

6.4.2. Sludge Cake Compressibility...

The value of r for most wastewater sludges changes with pressure according to the relationship ;

r = ( r O ) ( P S )

where ; r O : a constant and S : a coefficient of compressibility, which usually varies from 0.5 to 1.1.

Example 6-10 :

Determinations of r at different pressures give a slope of 0.65 for a plot of log r versus log P for sludge A. The value of r at 90 kN / m 2 is 1.5 x 10 13 m / kg for sludge A. A value quoted in the literature is 2.3 x 10 9 s 2 / g at 2,000 g / cm 2 for sludge B. Compare the dewaterability of the two sludges.

Calculation :

Literature value ( B ) : a pressure of 2,000 g / cm 2 is in effect ( 2,000 ) ( 981 ) dynes / cm 2 or 196 kN / m 2 and a r value of 2.3 x 10 9 s 2 / g is ( 2.3 x 10 9 ) ( 9,810 ) = 2.3 x 10 13 m / kg.

Determined value ( A ) : a value for r of 1.5 x 10 13 m / kg at 90 kN / m 2 is equivalent, at 196 kN, to ;

( r 196 / 1.5 x 10 13 ) = ( r O / r O ) ( 196 / 90 ) 0.65

or r 196 = 2.5 x 10 13 m / kg. The specific resistance of sludge B quoted in the literature is therefore lower than an equivalent value for sludge A. It should be noted that a standard pressure of 49 kN / m 2 ( 500 gf / cm 2 ) has often been used when quoting values of r in the literature.

6.5. Sludge Dewatering...

Three common methods of sludge dewatering are used ; vacuum filtration, pressure filtration and centrifugation. All operate on treated wastewater sludges in which the specific resistance has been reduced by a factor of 50 or more.

6.5.1. Vacuum Filtration...

Gale has suggested a formula relating yield from a vacuum filter ( shown below ) and specific resistance, i.e. ;

Y = { [ ( 2 P ) ( C L ) ( A F ) ] / [ ( MU ) ( r ) ( THETA R ) ] } 1 / 2 ( f C )

where ; Y : yield of dry SS ( kg / m 2 . s ), A F : fraction of filter area used in cake formation, i.e. that area below the sludge surface ( m 2 ), THETA R : time per revolution ( s ), C L : mass of solids / unit volume of liquid in the sludge ( kg / m 3 ) and f C : ( mass of liquid / unit mass of sludge ) / ( mass of filtrate obtained / unit mass of sludge dewatered ) or ;

f C = [ 1 - ( SC )( SL ) ] / [ ( 1 - SC( SL ) / ( SC )( C ) ]



where ; ( SC )( SL ) : solids content of the sludge ( kg / kg ) and ( SC )( C ) : solids content of the cake before drying begins, i.e. as the cake leaves the sludge bath.

Example 6-11 :

A vacuum filter is 2 m in diameter with cycle time of 150 s / revolution. The initial sludge solids content is 3 % and scraping of cake emerging from the sludge bath show 10 % SC. The filter dips 0.15 m into the sludge which is at 20 O C ( MU = 1 x 10 - 3 N . s / m 2 ). A pressure difference of 90 kN / m 2 is developed across the filter using a conditioned sludge with specific resistance 5 x 10 11 m / kg at 90 kN / m 2 . Calculate the filter yield.

Calculation :

f C = [ 1 - 0.03 ] / [ 1 - ( 0.03 / 0.10 ) ] = 1.39

C L = [ ( 0.03 ) / ( 1 - 0.03 ) ] ( 10 3 ) = 30.9 kg / m 3

From figure given above ;

A F = Cos - 1 ( 0.85 ) / 180 = 0.18

Therefore ;

Y = { [ ( 2 ) ( 90 ) ( 10 3 ) ( 30.9 ) ( 0.18 ) ] / [ ( 10 - 3 ) ( 5 x 10 11 ) ( 150 ) ] } 1 / 2 ( 1.39 ) = 5.1 x 10 - 3 kg / m 2 . s

The effect of using an unconditioned sludge with r = 5 x 10 13 is to reduce the yield to 5.1 x 10 - 3 kg / m 2 . s, all other values being held constant.

6.5.2. Pressure Filtration...

One empirical equation used in the determination of filter press drying of wastewater sludges is ;

T = { ( k ) ( r ) [ SC(F) - SC(SL) ] 2 } / { [ ( P ) ( SC(SL) ) ( 1 - SC(SL) ) ] }

where ; T : time to press to a specified final cake solids content SC(F) and k : constant. T is usually measured in hours. Values of k vary considerably, however, for the calculation below, k is taken as 1.3 x 10 - 6

Example 6-12 :

( a ) For a conditioned sludge of 3 % SC calculate the pressing times to obtain cakes of 20, 30 and 40 % SC given that P = 550 kN / m 2 and the specific resistance of the conditioned sludge, measured at 550 kN / m 2 , is 5 x 10 12 m / kg. Assume k = 1.3 x 10 - 6 .

( b ) Calculate the same values for input sludge solids of 5 % SC.

Calculation :

( a ) For SC(F) = 0.20 ;

T = [ ( 1.3 x 10 - 6 ) ( 5 x 10 12 ) ( 0.20 - 0.03 ) 2 ] / [ ( 550 x 10 3 ) ( 0.03 ) ( 1 - 0.03 ) ] = 11.7 h

For final cake solids of 30 % SC and 40 % SC the times are 29.6 and 55.6 h, respectively.

( b ) If the input sludge solids increases to 5 % solids after conditioning, the time to press to 20 % solids is given by ;

T = [ ( 1.3 x 10 - 6 ) ( 5 x 10 12 ) ( 0.20 - 0.05 ) 2 ] / [ ( 550 x 10 3 ) ( 0.05 ) ( 1 - 0.05 ) ] = 5.6 h

and times for final cake solids content SC(F) of 30 and 40 % for the same input would be 15.6 and 30.5 h, respectively.

Example 6-13 :

A sludge treated with ferric chloride gives a specific resistance value at 49 kN / m 2 of 10 12 m / kg ( S = 0.6 ) and when treated with cationic polyelectrolytes gives the same specific resistance at 49 kN / m 2 but with compressibility coefficient of S = 1.0. Calculate the ratio of the pressing times for the two sludges at a pressure of 700 kN / m 2 .

Calculation :

If S = 0.6 the specific resistance at 700 kN / m 2 will be ;

r 700 = ( 10 12 ) ( 700 / 49 ) 0.6 = 4.9 x 10 12 m / kg

for S = 1.0 ;

r 700 = ( 10 12 ) ( 700 / 49 ) 1.0 = 1.4 x 10 13 m / kg

Therefore, the ratio of the pressing times is given by ;

( T S = 0.6 ) / ( T S = 1.0 ) = ( 4.9 x 10 12 ) / ( 1.4 x 10 13 ) = 0.35

It is therefore clear that treatment of sludges with polyelectrolytes ( S = 0.9 - 1.1 ) gives too high a coefficient of compressibility to be used in high pressure filter presses. High pressure processes almost always use inorganic Al or Fe salts together with lime, as sludge conditioners ( S = 0.4 - 0.6 ).

6.6. Incineration...

Incineration of sludges, possibly mixed with domestic refuse, is often used where the water content can be lowered to a point where the combustion becomes autothermic, i.e. self - sustaining. In order to achieve efficient combustion it is necessary to add air of the stoichiometric requirement, this is referred to as excess air. For autothermic combustion the heat produced from the calorific value of the solids in the sludge less any heat losses must be sufficient to raise the moisture in the sludge cake to the exit temperature. The actual percentage of the heat available to do this depends upon the wall and ash losses and the heat lost in the gases emitted from the heat exchanger ( if fitted ).

6.6.1. Stoichiometric Oxygen Requirements...

Theoretical values for the oxygen required for combustion can be calculated from analytical data.

Example 6-14 :

Given the formula C 5 H 7 N O 2 for waste activated sludge, calculate the volume and mass of air required for combustion assuming 100 % excess air is needed.

Calculation :

For the above formula ve have ;

Element Number of atoms Atomic weight Total element mass / g molecular weight
Carbon 5 12 60
Hydrogen 7 1 7
Nitrogen 1 14 14
Oxygen 2 16 32
Total 113

or an analytical make up of 53.1 % C ; 6.2 % H ; 12.4 % N and 28.3 % O. Therefore, in 1 kg of combustible material ( CM ) we have approximately 0.53 kg C which reacts thus ;

C + O 2 ====> C O 2

12 g + 32 g ====> 44 g

or ;

( 0.531 kg C ) + ( 32 / 12 ) ( 0.531 kg O 2 )

i.e. 1.42 kg O 2 are required to burn the carbon. Similarly for hydrogen ;

H 2 + O ====> H 2 O

2 g + 16 g ====> 18 g

0.062 + 0.50

The 0.12 kg N requires no oxygen since it is emitted as N 2 gas. Therefore the oxygen requirement is ;

1.42 kg + 0.50 kg - 0.28 kg ( from sludge ) = 1.64 kg oxygen

At 100 % excess air, the oxygen in the excess air is 1.64 kg. At NTP, 22.4 L oxygen contains 32 g O 2 , therefore 1.64 kg is equivalent to 1.15 m 3 O 2 . In the air this is equivalent to ( 1.15 ) / ( 0.21 ) = 5.5 m 3 air.

Air Mass Calculation :

0.21 x 22.4 L oxygen contains 0.21 x 32 g O 2 and 0.79 x 22.4 L nitrogen contains 0.79 x 28 g N 2 . Thus 22.4 L air contains 6.72 g O 2 and 22.12 g N 2 . Thus in normal air, 1 kg O 2 is associated with 22.12 / 6.72 kg N 2 or ( 22.12 + 6.72 ) / ( 6.72 ) kg air ; i.e. 1 kg O 2 is equivalent to 3.29 kg N 2 or 4.29 kg air. Thus 1.64 kg O 2 = 7.04 kg air. Therefore, in total, 3.28 kg O 2 are required for input in the form of 11.0 m 3 air / kg combustible material or 14.1 kg air / kg combustible material.

6.6.2. Heat Budget...

Knowing the specific heats of the N 2 , air, C O 2 etc. in the exit gas, and estimating the wall, ash and other heat losses enables a heat budget calculation to be carried out. The heat H required to raise 1 kg water from an inlet temperature T I to an exit temperature T E where T E > 100 O C is approximately ;

H = ( 4.18 ) ( 100 - T I ) + 2,257 + ( 2.09 ) ( T E - 100 ) kJ

where the 2,257 kJ is the latent heat of vaporization of water. If 1 kg of combustible material has a calorific value of K ( kJ / kg CM ), and Z is the fraction of heat from this calorific value which is lost at walls, in ash and exit gases etc., the mass of water which may be raised to the exit temperature is ( 1 - Z ) ( K / H ) kg H 2 O per kg CM incinerated. This can be used to calculate whether a sludge of given SC will burn without extra fuel.

Example 6-15 :

A mixed sludge has a calorific value of 22,000 kJ / kg CM, is 80 % organic and has been dewatered to 75 % MC. Calculate whether autothermic combustion is possible :

( a ) Assuming 40 % heat loss with a heat exchanger producing an exit temperature of 450 O C
( b ) Assuming 60 % heat loss with no heat exchanger and an exit temperature of 800 O C

Calculation :

The heat required to raise 1 kg water to an exit temperature of 450 O C from, say , 15 O C, is ;

H 450 = ( 4.18 ) ( 100 - 15 ) + 2,257 + ( 2.09 ) ( 450 - 100 ) = 3,340 kJ

and similarly to 800 O C ( H 800 ) is 4,080 kJ. In case ( a ) ( 0.60 ) ( 22,000 ) = 13,200 kJ / kg CM is available after losses, i.e. there is sufficient heat to raise ( 13,200 ) / ( 3,340 ) = 3.95 kg H 2 O to 450 O C. Therefore if 1 kg CM ( or 1 kg organics ) is associated with 3.95 kg H 2 O, the sludge will just continue to support combustion. Now, 1 kg organics is associated with ( 0.20 / 0.80 ) = 0.25 kg inorganics for a sludge which is 80 % organic material. Thus the composition of sludge which will just support autothermic combustion is ;

( 1 + 0.25 ) / ( 1.25 + 3.95 ) = 0.24 ( 24 % SC )

i.e. the 75 % MC sludge satisfies the conditions. For condition ( b ) the heat available is 8,800 kJ and this is equivalent to 2.16 kg H 2 O. Thus the cake composition would have to be ;

( 1.25 ) / ( 1.25 + 2.16 ) = 0.37 ( 37 % SC )

Autothermic combustion cannot be sustained with a sludge of 75 % MC and in this case the temperature would gradually drop ( unless extra fuel were added ) until combustion ceased.

6.7. Return Liquor Streams...

In many forms of sludge treatment a highly polluting liquor is produced which is pumped back to the works inlet in some cases exerting a significant BOD or SS load. Detailed calculations of loads for a wide range of sludge treatment processes have been presented elsewhere. Table shown below gives values of BOD and SS, which although showing wide variations in practice, may be used for illustration. In the following examples the per capita daily production of BOD and SS are taken as 0.060 kg and 0.090 kg, respectively.

Process BOD concentration ( mg / L ) SS concentration ( mg / L )
Filter press ( raw sludge ) 2,000 200
Filter press ( conditioned raw sludge ) 1,800 150
Filter press ( heat conditioned sludge ) 6,000 200
Filter press ( digested sludge ) 1,400 100
Drying beds ( digested sludge ) 100 150
Vacuum filtration liquors have similar concentrations to those for filter presses, however, the final SC is less than 25 %.

Example 6-16 :

A conditioned sludge is pressed from 6 % to 40 % SC producing a liquor containing 1,800 mg / L BOD. Calculate the increased inlet BOD load and secondary BOD load owing to return of the liquid stream.

Calculation :

The liquor change per kg dry sludge solids is given by ;

[ ( 100 / 6 ) - 1 ] - [ ( 100 / 40 ) - 1 ] = 14.2 kg liquor

or for 0.09 kg solids / day, 1.28 kg, i.e. 1.3 L / capita . day. At 1,800 mg / L BOD this represents ( 1,800 ) ( 1.3 x 10 - 6 ) = 0.0023 kg BOD / capita . day or approximately 3.8 % of the inlet BOD. However, since most would pass through the primary settlement tank, the load on the secondary processes, assuming 40 % removal of the inlet BOD, would be increased by [ ( 0.0023 ) / ( 0.60 ) ( 0.06 ) ] ( 100 % ) = 6.4 %. Heat treatment liquors can be particularly troublesome.

Example 6-17 :

The sludge in this example is heat treated at 5 % SC prior to filter pressing to 45 % SC. Assuming the filtrate to contain 6,000 mg / L BOD, calculate the increased BOD load to the secondary processes.

Calculation :

The overall liquid change for 0.09 kg solids input is ;

{ [ ( 100 / 5 ) - 1 ] - [ ( 100 / 45 ) - 1 ] } ( 0.09 ) kg or 1.6 L / capita . day

The BOD load is ( 1.6 ) ( 6,000 x 10 - 6 ) = 0.0096 kg BOD / capita . day, which, compared with 0.036 kg / capita . day BOD in the flow after primary settlement represents an increased loading of 27 %. In this case, should the liquor be returned too rapidly to the works inlet, it could overload the secondary plant.

6.8. Conditioning of Sludges...

Sludges are usually conditioned prior to vacuum filtration, centrifugation or filter pressing. Since sludges vary in source, type, composition and alkalinity, the majority of processes are based upon local, empirical data. One common conditioning process is the use of chemicals, which are usually added as a percentage of the dry sludge solids. Common chemicals include Al 2 ( OH ) 4 Cl 2 , Al Cl 3 , Fe Cl 3 , Fe Cl 3 + Fe 2 ( SO 4 ) 3 mixture and lime and copperas.

Example 6-18 :

A sludge of 4 % SC is to be conditioned using a lime and copperas mixture, the lime slurry and the copperas solution contain 10 % lime and 25 % copperas w / v, respectively. Calculate the volumes of slurry and solution required to dose 10 m 3 sludge at 15 % of the sludge dry solids content. The ratio of lime to copperas is 5 : 3 as dry weights.

Calculation :

At 4 % SC 10 m 3 sludge contains approximately 10 x 40 = 400 kg dry solids. At 15 % of dry solids, 0.15 x 400 = 60 kg total lime and copperas solids are required, i.e. ( 5 / 8 ) ( 60 ) = 37.5 kg lime and ( 3 / 8 ) ( 60 ) = 22.5 kg copperas. A lime slurry of 10 % w / v contains 100 kg / m 3 and hence, 37.5 / 100 = 375 L of lime slurry is required together with 22.5 / 250 = 90 L of copperas solution. Because Fe Cl 3 is not commonly available in commercial quantities it is sometimes necessary to oxidize copperas to the ferric state by using chlorine to produce a mixture of Fe Cl 3 and Fe 2 ( SO 4 ) 3 according to the expression ;

6 Fe SO 4 . 7 H 2 O + 3 Cl 2 = 2 Fe Cl 3 + 2 Fe 2 ( SO 4 ) 3 + 42 H 2 O

The minimum amount of Cl 2 necessary can be calculated from the above expression.

Example 6-19 :

Calculate the stoichiometric ( minimum ) amount of Cl 2 necessary to treat 500 L of 25 % copperas solution.

Calculation :

The molecular weights of Fe SO 4 . 7 H 2 O and Cl 2 are 55.9 + 32.1 + 64.0 + 7 x 18 = 278.0 for Fe SO 4 . 7 H 2 O and 2 x 35.5 = 71.0 Cl 2 gas. Thus 278 g Fe SO 4 . 7 H 2 O requires 71.0 g Cl 2 x ( 3 / 6 ) = 125 kg copperas and would require ( 125 / 278 ) ( 35.5 ) = 16.0 kg Cl 2 .