( dD / dt ) = ( K 1 ) ( L ) - ( K 2 ) ( D )
i.e. the oxygen deficit will be increased by increasing the polluting load L and diminished by reaeration. Although this model neglects the effects of photosynthetic oxygen production ( by algae ) and the oxygen depletion by benthic ( bottom ) deposits, it can be surprisingly accurate, since these two neglected effects often cancel out. Streeter and Phelphs also showed that, by integrating the equation given just above, a general equation for the dissolved oxygen deficit at any time t could be written, namely ;
D = { [ ( k 1 ) / ( k 2 - k 1 ) ] ( L A ) [ 10 ( - k 1 ) ( t ) - 10 ( - k 2 ) ( t ) ] } + ( D A ) [ 10 ( - k 2 ) ( t ) ]
The general form of the equation is a " sag " curve.
Example 7-3 :
If k 1 and k 2 for a given river are 0.15 1 / day and 0.20 1 / day, respectively, calculate the dissolved oxygen deficits for the flow 6 days downstream if the river is initally 80 % saturated and has an ultimate BOD of 10 mg / L. The value of C S for the river is 12 mg / L.
Calculation :
For day 0 ;
D A = ( 0.20 ) ( 12 ) = 2.4 mg / L
For day 1 ;
D 1 = { [ ( 0.15 ) / ( 0.20 - 0.15 ) ] ( 10 ) [ 10 ( - 0.15 ) - 10 ( - 0.20 ) ] } + ( 2.4 ) [ 10 ( - 0.20 ) ] = 3.82 mg / L
For day 2 ;
D 2 = { [ ( 0.15 ) / ( 0.20 - 0.15 ) ] ( 10 ) [ 10 ( - 0.30 ) - 10 ( - 0.40 ) ] } + ( 2.4 ) [ 10 ( - 0.40 ) ] = 4.05 mg / L
Similarly, D 3 = 3.71 mg / L, D 4 = 3.16 mg / L, D 5 = 2.57 mg / L and D 6 = 2.04 mg / L. The shape of the curve of C versus time is shown in figure given below, which clearly indicates a minimum DO concentration somewhere around 1.7 to 1.8 days.
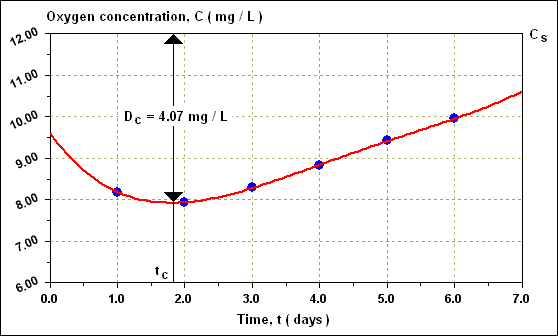
This critical value of the dissolved oxygen deficit D C which is reached at time t C occurs when ( dD / dt ) = 0 in the equation. Hence, putting D C = D and L = ( L A ) [ 10 ( - k 1 ) ( t C ) ] it can be shown that ;
D C = ( k 1 / k 2 ) ( L A ) [ 10 ( - k 1 ) ( t C ) ]
and occurs at ;
t C = [ 1 / ( k 2 - k 1 ) ] log 10 { ( k 2 / k 1 ) { 1 - ( D A / L A ) [ ( k 2 - k 1 ) / ( k 1 ) ] } }
For the conditions in the last example ;
t C = [ 1 / ( 0.20 - 0.15 ) ] log 10 { ( 0.20 / 0.15 ) { 1 - ( 2.4 / 10 ) [ ( 0.20 - 0.15 ) / ( 0.15 ) ] } } = 1.77 days
and ;
D C = ( 0.15 / 0.20 ) ( 10 ) [ 10 ( - 0.15 ) ( 1.77 ) ] = 4.07 mg / L
Example 7-4 :
A town discharges 0.05 m 3 / s of settled sewage with a BOD 5 of 150 mg / L ( for which the reaction rate is 0.17 1 / day at 20 O C ) into a river which has a minimum flow of 0.30 m 3 / s. The temperatures of the river and effluent are 15 O C and k 1 and k 2 for the river are found to be 0.20 1 / day and 0.30 1 / day by experiment, respectively. The dissolved oxygen contents of the effluent and river are 2.1 and 9.4 mg O 2 / L, respectively, prior to mixing and the BOD ultimate of the river is 2 mg / L. Calculate the magnitude of the critical dissolved oxygen deficit and the time at which it occurs.
Calculation :
For the sewage BOD 5 test ;
L O ( 20 O C ) = ( 150 ) / [ 1 - 10 ( - 0.17 ) ( 5 ) ] = 175 mg / L
Correcting L O to 15 O C gives ;
L O ( 15 O C ) = ( 175 ) [ 1 + ( 0.02 ) ( 15 - 20 ) ] = 158 mg / L
For the stream dilution of BOD ;
( 158 ) ( 0.05 ) + ( 2.0 ) ( 0.30 ) = ( L A ) ( 0.05 + 0.30 )
Thus ;
L A = 24.3 mg / L
For the stream dilution of dissolved oxygen ;
( 2.1 ) ( 0.05 ) + ( 9.4 ) ( 0.30 ) = ( C ) ( 0.05 + 0.30 )
C = 8.36 mg / L
The value of C S at 15 O C for fresh water is 10.2 mg / L ; thus D A = 10.2 - 8.4 = 1.8 mg / L. Thus ;
t C = [ 1 / ( 0.30 - 0.20 ) ] log 10 { ( 0.30 / 0.20 ) { 1 - ( 1.8 / 24.3 ) [ ( 0.30 - 0.20 ) / ( 0.20 ) ] } } = 1.60 days
and ;
D C = ( 0.20 / 0.30 ) ( 24.3 ) [ 10 ( - 0.20 ) ( 1.60 ) ] = 7.75 mg / L
Fair has proposed modifying Streeter and Phelphs equation by using a cipher f to represent ( k 2 / k 1 ). The time t C then becomes ;
t C = [ 1 / ( k 1 ) ( f - 1 ) ] log 10 { ( f ) [ 1 - ( D A / L A ) ( f - 1 ) ] }
and ;
D C = ( L A / f ) [ 10 ( - k 1 ) ( t C ) ]
