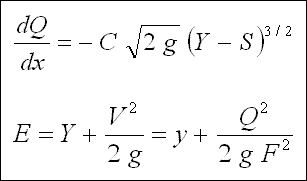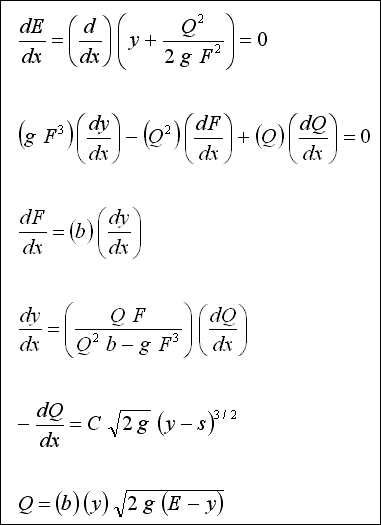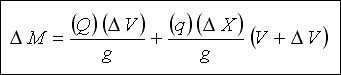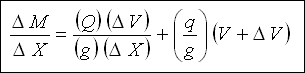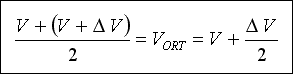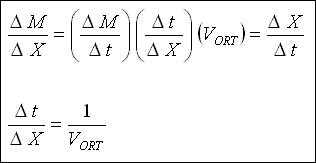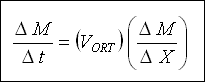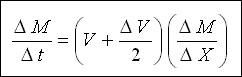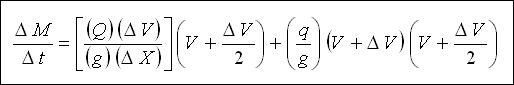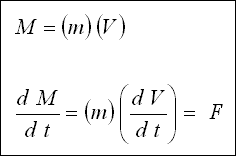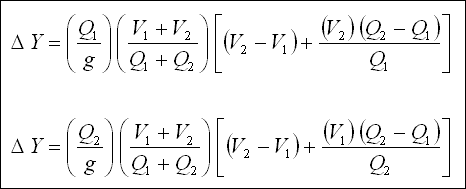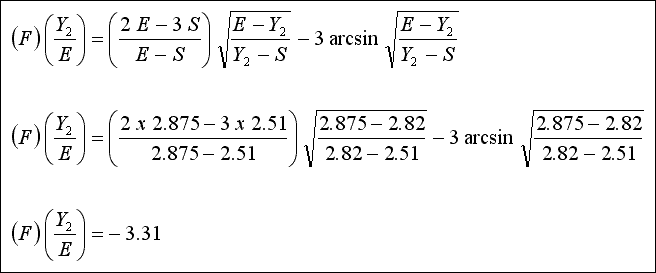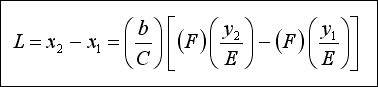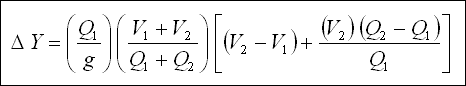Türkçe metni rahat izleyebilmeniz için, "browser" ınızın "document encoding" ini "Turkish" olarak değiştirdiniz mi ? ...
Yan Savakların Tasarım Kriterleri ve Tasarım Örnekleri...

Büyültmek için tıklayınız...
© 2006 "Toprak Home Page"...
Yan Savaklar...
Genel...
Ana kanal su seviyesinde hava paylarını aşan bir artış olduğunda, su seviyesini kontrol etmek dolayısı ile kanalları
korumak amacı ile uygun bir tahliye olanağı veren yerlerde kanal eksenine paralel olarak yan savak inşa edilir. Yan savak
kret kotu olarak, kanal proje debisine karşılık gelen seviyeden genellikle bir kaç santim yukarıda olan bir seviye alınır.
Savak Kreti Üzerindeki Su Profili...
Yan savaklarda, savak üzerinden aşan su napının savak boyunca meydana gelecek serbest yüsey çizgisi kanaldaki rejime göre
oluşur. Aşağıda savak üzerinde oluşabilecek 5 durum gösterilmiştir.

( a ) Tipi : Savak başlangıcında veya yakınında kritik akım koşulları oluşur. Akım savak boyunca sel rejimindedir
ve su derinliği savak boyunca azalır.
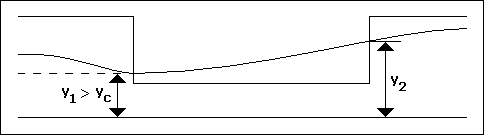
( b ) Tipi : Savak başlangıcında su derinliği kritik derinlikten büyüktür. Akım savak boyunca nehir rejimindedir
ve su derinliği savak boyunca artar.
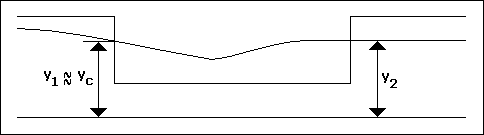
( c ) Tipi : Savak başlangıcında ( a ) tipi akım vardır. Savak kesitinde oluşan hidrolik sıçramadan sonra ( b ) tipi
akım hakim olur. ( b ) tipi akım sıçrama kayıplarından dolayı daha düşük bir özgül enerjiye sahiptir.

( d ) Tipi : Savak başlangıcında su derinliği kritik derinlikten küçüktür. Akım savak boyunca sel rejimindedir
ve su derinliği savak boyunca azalır.
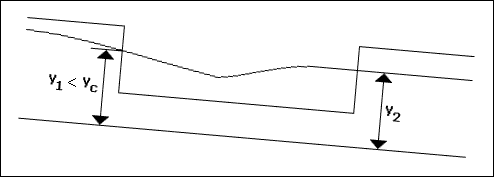
( e ) Tipi : Savak başlangıcında ( d ) tipi akım vardır.
( d ) ve ( e ) tipleri gelen akım sel rejiminde ise oluşur. Yan dolu savaktaki hız genellikle savağa dik olarak kabul
edilir. Bu kabul nehir rejimindeki akımlar için, sel rejimindeki akımlardan daha doğrudur. Sel rejimli akımlarda hız
büyüktür ve bunun sonucu olarak ( d ) ve ( e ) tiplerinin başarı ile analizi kolay değildir. Ayrıca, ( d ) ve ( e )
tiplerinde debi menba şartları ile kontrol edildiğinden bunu da dikkate almak gerekir.
Savak Debisi...
1934 yılında " Marchi " yan savaklar için aşağıdaki kabulleri yaparak deneysel araştırmalarda bulunmuştur.
- Yan savak üzerinde özgül enerji sabittir.
- Kanaldaki akım üniformdur.
- Kanal çok uzun ve kesiti sabittir.
- Savak kreti kanal tabanına paraleldir.
- Kısa mesafelerde normal savak formülleri yan savaklara da uygulanabilir.
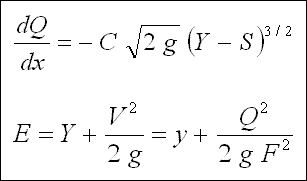
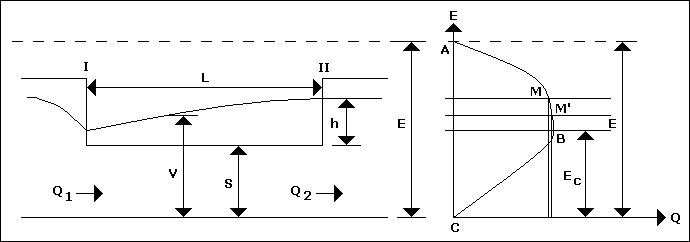
Sabit enerji parabolünden görüleceği üzere, kanaldaki akım nehir rejiminde ise, yani " B " noktasının üzerinde debi
azaldıkça su seviyesinde yükselme olacaktır. Kanaldaki akım sel rejiminde ise, yani " B " noktasının altında debi
azaldıkça su seviyesinde azalma olacaktır.
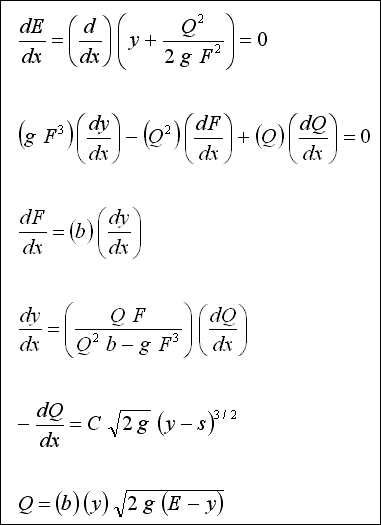

( F ) ( Y / E ) fonksiyonu yan savak karakteristiği olarak tanımlanır. Bu fonksiyon S < y < E değerleri arasında realdir.
C = ( 2 / 3 ) ( RO ) olup, RO 0.73 ile 0.85 arasında değişir ve tipik bir değer olarak C = 0.57 - 0.62 alınabilir.
Yan Savak Kanalı...
Kret üzerinden dökülen su ; kanalda mevcut su ile karıştığı anda ; kanal eksenine dik bir hız bileşenine sahip ise de ;
bu hızın kanal ekseni boyuncasu hareketi üzerinde bir etkisi olmadığı ve dökülen suyun enerjisinin kanal akışına karışarak
kırıldığı, kanaldaki hareketi doğuran yegane kuvvetin kanal ekseni boyunca su seviyesindeki azalma olduğu kabul edilir.
Mekanikteki " Momentumun Korunumu Prensibi "ni kısa uzunluktaki bir yan kanal parçasına uygularsak, kanal parçasının
başlangıcındaki momentum ile dış kuvvetlerden dolayı momentum artışının toplamı parçanın sonundaki momentuma eşit olmalıdır.
Eğer kanal parçasının uzunluğu DELTA X ve menbadaki hız ve debi V ve Q ile gösterilirse, mansapta hız ve debi, sırası ile
( V + DELTA V ) ve ( Q + q . DELTA X ) olacaktır. q yan savağın birim boyundan geçen debidir. Buna göre ;
Menbada ; (Denklem 1)

Mansapta ; (Denklem 2)

Denklem 2'den Denklem 1'i çıkarırsak ;
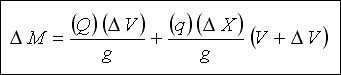
DELTA X ile bölündüğünde (Denklem 3) ;
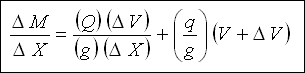
Göz önüne alınan ( DELTA X ) kanal parçasında ortalama akım hızı ;
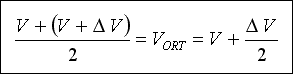
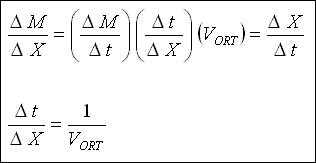

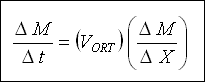
Denklem 4 ;
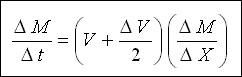
Denklem 4 Denklem 3'te yerine yazılacak olursa ;
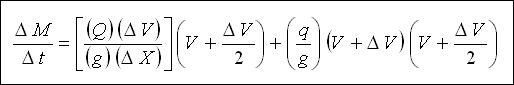
Bilindiği üzere, momentumun zamana göre değişimi kuvvete eşit olup bu kuvvet akışa paralel ve ivme kazandırıcı
yöndedir.
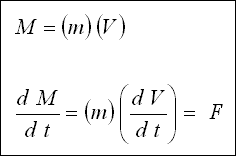
Aşağıdaki şekil incelenecek olursa, F kuvveti Q ağırlığının bileşenidir ;



Eğer Q 1 , V 1 ve Q 2 , V 2 göz önüne alınan kısa kanal parçasının başlangıç
ve sonundaki debi ve hızlar ise, sırası ile, aşağıdaki Denklem 5 ve 6 yazılabilir ;
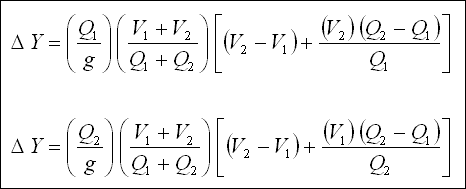
Denklem 5 veya 6'nın çözümü deneme - yanılma yöntemi ile yapılabilir ( Sayısal örnekte verilmiştir ).
Kırılma Noktasının Yerinin Saptanması...
Su hattı hesaplarına, bilinen bir su derinliğinden başlanır ve bu nokta " kontrol noktası " olarak tanımlanır. Az eğimle
gelen bir kanalın eğimi aniden artar ise, eğim değişimi olan bu noktada veya düşey bir şütte şüt başlangıcında kritik
derinlik oluşur ve bu nokta kontrol noktasıdır. Kesiti dikdörtgen olmayan ve debisi devamlı değişen kanallarda konu
oldukça karmaşıktır ve kontrol kesiti kanalda herhangi bir noktada oluşabilir. Aşağıda, kontrol noktasının saptanması için
" Julian Hinds " tarafından verilen bir yöntem açıklanmış ve sayısal bir örnek ile yöntemin uygulanması gösterilmiştir.
Sayısal Örnek...
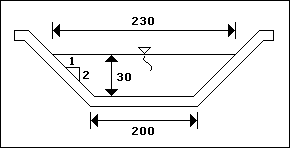
Kesiti ve hidrolik özellikleri aşağıda verilen Q = 40 m 3 / sn'lik bir kanal üzerinde, Q SAVAK =
10 m 3 / sn kapasiteli bir yan savak inşa edilecektir. ( a ) Yan savak boyunu hesaplayınız ve ( b ) Yan savak
kanalında su profilini saptayarak kanalda nehir rejimi oluşup oluşmadığını kontrol ediniz.
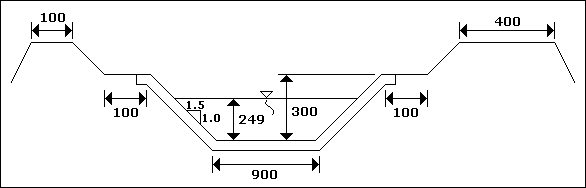
( b : kanal taban genişliği, d : kanaldaki su derinliği H 1 : toplam kanal yüksekliği )
| Q ( m 3 / sn ) |
n |
l |
b ( m ) |
d ( m ) |
A ( m 2 ) |
V ( m / sn ) |
H 1 ( m ) |
| 40 |
0.016 |
0.0002 |
9.00 |
2.49 |
31.75 |
1.29 |
3.00 |
Yan Savak Boyunun Hesaplanması...
- Q = Q KANAL + Q SAVAK = 40 + 10 = 50 m 3 / sn
- 50 m 3 / sn için özellikleri yukarıda verilen kanaldaki normal su derinliği Y 1 = 2.78 m, akım hızı
V 1 = 1.365 m / sn ve hız yüksekliği ; hv 1 = ( V 1 2 ) / ( 2 x g ) =
0.095 m
- Enerji yüksekliği = E = Y 1 + hv 1 = 2.875 m
- Yan savak mansabında özgül enerji sabit kalacak fakat debi 50 m 3 / sn'den 40 m 3 / sn'ye
düşecektir.
- E = Y 1 + hv 1 = Y 2 + hv 2 = Y 2 +
( Q 2 ) / [ ( 2 x g ) ( 1.5 x Y 2 + 9.00 ) 2 ( Y 2 ) ] = 2.875 m ====>
Y 2 = 2.82 m
- Yan savak kreti 40 m 3 / sn için kanalda oluşan su seviyesinin 2 cm üzerinde olacaktır. Bu durumda,
S = 2.49 + 0.02 = 2.51 m'dir.
- Savak üzerindeki toplam yük = E - S = 2.875 - 2.510 = 0.365 m
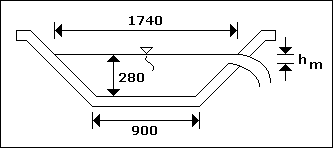
- Savak üzerinde su hattı yükselmesini lineer olarak kabul edersek ; Y m =
( Y 1 + Y 2 ) / 2 = 2.80 m
- Ortalama savak yükü = Y m - S = 2.80 - 2.51 = 0.29 m
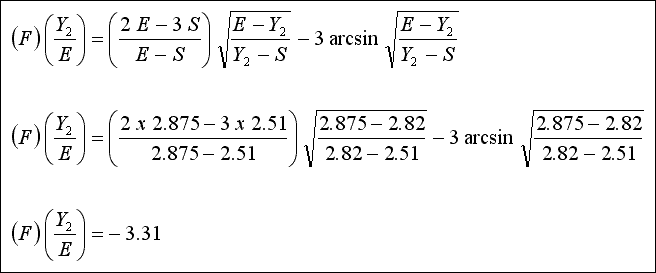

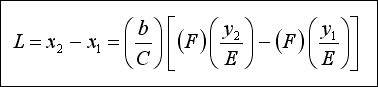
- Ortalama yükte su yüzeyi genişliği, b = 17.40 m
- Savak katsayısı, c = 0.57 olarak alınabilir
- L = ( 17.40 / 0.57 ) ( - 3.31 + 4.67 = 1.36 ) = 41.52 ====> 40 m
Yan Savak Kanalının Hesabı...
Kanal içinde iyi hidrolik şartların sağlanması için akımın nehir rejiminde olması gerekir. Seçilen S = 0.01 taban eğimi
için bunun sağlanıp sağlanmadığı araştırılmış ve kanal içinde su profili daha önce açıklandığı gibi hesaplanmıştır. Kanalın
kesiti aşağıdaki şekilde verilmiştir.
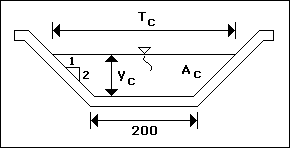
Kesiti yukarıdaki şekilde verilen kanalda çeşitli kritik su derinlikleri için debiler hesap edilmiştir. Kritik derinlikler
için genel denklem ;
Qc 2 / g = Ac 3 / Tc'dir. Burada Ac kritik derinlikte ıslak kesit alanı, Tc ise su yüzeyi
genişliğidir. Qc = ( Ac ) ( Vc ) ve hvc = Vc 2 / 2 x g ( kritik derinlikte hız yüksekliği ) olduğuna göre ;
( Ac 2 ) ( Vc 2 ) / g = Ac 3 / Tc ve Vc 2 / 2 x g = Ac / 2 x Tc
Ac = ( 2.00 + 0.50 x Yc ) ( Yc ) ve Tc = ( 2.00 + Yc )
Çeşitli Yc değerleri için yapılan hesaplar aşağıdaki tabloda özetlenmiştir.
| Y |
A |
T |
A / 2 T |
Vc |
Qc |
Rc |
| 0.20 |
0.42 |
2.20 |
0.095 |
1.36 |
0.570 |
0.172 |
| 0.30 |
0.645 |
2.30 |
0.140 |
1.66 |
1.070 |
0.242 |
| 0.40 |
0.88 |
2.40 |
0.183 |
1.89 |
1.665 |
0.304 |
| 0.60 |
1.38 |
2.60 |
2.265 |
2.28 |
3.150 |
0.413 |
| 0.80 |
1.92 |
2.80 |
0.345 |
2.60 |
5.000 |
0.506 |
| 1.00 |
2.50 |
3.00 |
0.416 |
2.85 |
7.130 |
0.590 |
| 1.20 |
3.12 |
3.20 |
0.488 |
3.09 |
9.650 |
0.666 |
| 1.40 |
3.78 |
3.40 |
0.556 |
3.30 |
12.480 |
0.737 |
| 1.60 |
4.48 |
3.60 |
0.622 |
3.49 |
15.650 |
0.803 |
| 1.80 |
5.22 |
3.80 |
0.686 |
3.68 |
19.200 |
0.868 |
| 2.00 |
6.00 |
4.00 |
0.750 |
3.83 |
23.000 |
0.926 |
| 2.20 |
6.85 |
4.20 |
0.815 |
4.00 |
27.400 |
1.000 |
40 m uzunluğundaki yan savak kanalı 5'er m'lik kısımlara bölünerek ;
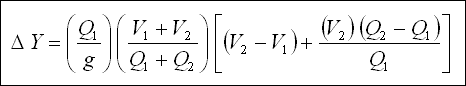
formülü ile, her noktasında kritik derinliğe sahip olan, fiktif bir kanalda su profili hesabı aşağıdaki tabloda
verilmiştir. Tablodaki her kolonun açıklaması aşağıda sunulmuştur.
Kolon - 01 : Başlangıç kesitinden mesafe ( m )
Kolon - 02 : Mesafe farkı ( m )
Kolon - 03 : Göz önüne alınan kanal parçasından geçen debi ( birim debi ile DELTA X mesafesinin çarpımı )
( m 3 / sn )
Kolon - 04 : Göz önüne alınan kesitteki debi ile bir önceki kesitteki debilerin toplamı ( m 3 / sn )
Kolon - 05 : Kolon - 3'teki debiye karşılık gelen yukarıdaki tablodan enterpolasyon ile bulunan kritik derinlik
( m )
Kolon - 06 : Tablodan enterpolasyon ile bulunan ve Kolon - 3'teki debiye karşılık gelen kritik hız ( m / sn )
Kolon - 07 : Göz önüne alınan kesit ile bir önceki kesitteki hızların toplamı ( m / sn )
Kolon - 08 : Debideki artış, DELTA Q = Q 2 - Q 1
Kolon - 09 : Hızdaki artış, DELTA V = V 2 - V 1
Kolon - 10 : Yukarıdaki formül ile hesaplanan su yüzeyindeki alçalma ( m )
Kolon - 11 : Tablodan enterpolasyon ile bulunan ve Kolon - 3'teki debiye karşılık gelen kritik hidrolik yarıçap
( m )
Kolon - 12 : Sürtünme katsayısı n = 0.016 alınarak Kolon - 6'daki V hızından ve Kolon - 11'deki R hidrolik
yarıçapından yararlanılarak bulunan sürtünme kaybı, bu kayıp tablo değerlerinden de görülebileceği üzere oldukça küçük
olup ihmal edilebilir ( m )
Kolon - 13 : Su yüzeyindeki toplam alçalma, DELTA Y' = Y'm + hf ( m )
Kolon - 14 : Başlangıç kesitinden itibaren su yüzeyindeki toplam alçalma ( m )
| X |
DELTA X |
Q |
Q 1 + Q 2 |
Y c |
V c |
V 1 + V 2 |
DELTA Q |
DELTA V |
Y m |
R c |
h f |
DELTA Y' |
Toplam DELTA Y' |
| 01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
13 |
14 |
| 0 + 000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
| 0 + 005 |
5 |
1.25 |
1.25 |
0.33 |
1.73 |
1.73 |
1.25 |
1.73 |
- |
0.261 |
0.020 |
- |
- |
| 0 + 010 |
10 |
2.50 |
3.75 |
0.51 |
2.11 |
3.84 |
1.25 |
0.38 |
0.325 |
0.365 |
0.019 |
0.344 |
0.344 |
| 0 + 015 |
15 |
3.75 |
6.25 |
0.66 |
2.38 |
4.49 |
1.25 |
0.27 |
0.267 |
0.443 |
0.017 |
0.284 |
0.628 |
| 0 + 020 |
20 |
5.00 |
8.75 |
0.80 |
2.61 |
4.99 |
1.25 |
0.23 |
0.240 |
0.506 |
0.016 |
0.256 |
0.884 |
| 0 + 025 |
25 |
6.25 |
11.25 |
0.92 |
2.75 |
5.36 |
1.25 |
0.14 |
0.201 |
0.555 |
0.016 |
0.217 |
1.101 |
| 0 + 030 |
30 |
7.50 |
13.75 |
1.03 |
2.89 |
5.64 |
1.25 |
0.14 |
0.188 |
0.601 |
0.016 |
0.204 |
1.339 |
| 0 + 035 |
35 |
8.75 |
16.25 |
1.13 |
3.00 |
5.89 |
1.25 |
0.11 |
0.169 |
0.639 |
0.016 |
0.185 |
1.524 |
| 0 + 040 |
40 |
10.00 |
18.75 |
1.22 |
3.12 |
6.12 |
1.25 |
0.12 |
0.165 |
0.675 |
0.015 |
0.180 |
1.704 |
Her noktasında kritik derinliğe sahip olan kanaldaki su ve taban profili aşağıdaki şekilde şematik olarak gösterilmiştir.
Bu kanal profili ile S = 0.01 eğimli kanal kıyaslanacak olursa, görülür ki, her noktada kanal eğimi kritik eğimden
küçüktür ve yan savak kanalında nehir rejimi hakimdir.
- Yan savak kanalı sonunda 0.30 m yüksekliğinde bir eşik bulunmaktadır.
- Bc = 2.00 + 2 x 0.50 x 0.30 = 2.30 m
- dc = 1.14 m, hv = 0.48 m ve S = 0.30 m
- H = 1.14 + 0.48 + 0.30 = 1.92 m
- Kontrol kesitinin menbaında su derinliği ; du + Dvu = dc + hvc + S = 19.92 m ( eşik kaybı ihmal edilmiştir )
- du = 1.94 m
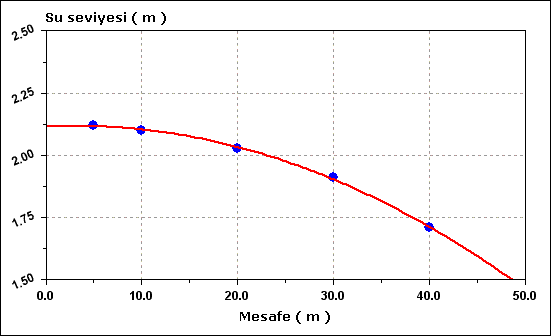
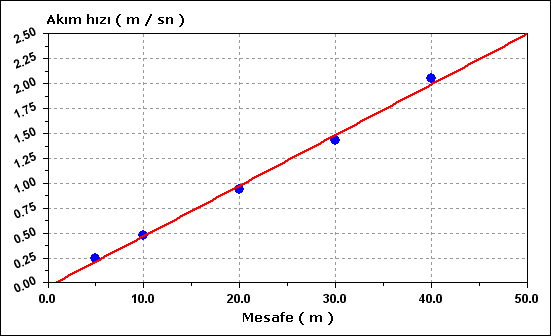
- Bilinen su derinliğinden hareket ederek kanalda su profili hesabı aşağıdaki tablo üzerinde yapılmıştır
| Km |
DELTA X |
Taban
kotu |
DELTA YKABUL |
Su
seviyesi |
d |
A |
Q |
V |
Q1+Q2 |
Q1/
( Q1+Q2)(g) |
V1+V2 |
V2-V1 |
Q2-Q1 |
(Q2-Q1)/
Q1 |
(V2)(Q2-Q1)/
Q1 |
13+16 |
DELTA YHESAP |
Sonuç |
| 01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 0+040 |
- |
0.00 |
- |
1.71 |
1.71 |
4.88 |
10 |
2.05 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
| 0+030 |
10 |
0.10 |
0.20 |
1.91 |
1.81 |
5.26 |
7.5 |
1.43 |
17.50 |
0.0437 |
3.48 |
0.62 |
2.50 |
0.333 |
0.68 |
1.30 |
0.20 |
Tam |
| 0+020 |
10 |
0.20 |
0.12 |
2.03 |
1.83 |
5.33 |
5.00 |
0.94 |
12.50 |
0.0407 |
2.37 |
0.49 |
2.50 |
0.500 |
0.72 |
1.21 |
0.12 |
Tam |
| 0+010 |
10 |
0.30 |
0.07 |
2.10 |
1.80 |
5.22 |
2.50 |
0.48 |
7.50 |
0.0340 |
1.42 |
0.46 |
2.50 |
1.00 |
0.94 |
1.40 |
0.07 |
Tam |
| 0+005 |
5 |
0.35 |
0.02 |
2.12 |
1.77 |
5.11 |
1.25 |
0.25 |
3.75 |
0.0340 |
0.73 |
0.23 |
1.25 |
1.00 |
0.48 |
0.71 |
0.02 |
Tam |