Activated Sludge Process Kinetics...
Biochemical Reactions...
Operationally, biological waste treatment with the activated sludge process is typically accomplished using a flow diagram
such as that shown below.
 "Schematic of Complete - Mix Reactor"...
"Schematic of Complete - Mix Reactor"...
Organic waste is introduced into a reactor where an aerobic bacterial culture is maintained in suspension. The reactor
contents are referred to as the "mixed liquor". In the reactor, the bacterial culture carries out the conversion in general
accordance with the stoichiometry shown in the equations given below ;
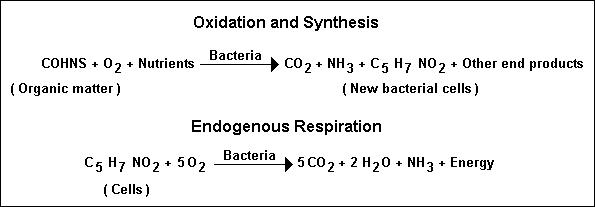
In these equations, COHNS represents the organic matter in wastewater. Although the endogenous respiration reaction
results in relatively simple end products and energy, stable organic end products are also formed. From equation given
above, it can be seen that, if all of the cells can be oxidized completely, the ultimate BOD of the cells is equal to
1.42 times the concentration of cells.
Cell Growth...
In both batch and continuous culture systems the rate of growth of bacterial cells can be defined by the following
relationship ;

where ; rg : rate of bacterial growth, m : specific growth rate and X : concentration of microorganisms.
Because dX / dt = rg for batch culture, the following relationship is also valid for a batch reactor ;
 Substrate Limited Growth...
In a batch culture, if one of the essential requirements (substrate and nutrients) for growth were present in only limited
amounts, it would be depleted first and growth would cease. In a continuous culture, growth is limited. Experimentally,
it has been found that the effect of a limiting substrate or nutrient can often be defined adequately using the following
expression proposed by Monod ;
Substrate Limited Growth...
In a batch culture, if one of the essential requirements (substrate and nutrients) for growth were present in only limited
amounts, it would be depleted first and growth would cease. In a continuous culture, growth is limited. Experimentally,
it has been found that the effect of a limiting substrate or nutrient can often be defined adequately using the following
expression proposed by Monod ;

where ; m : specific growth rate, mmax : maximum specific growth rate, S : concentration of growth - limiting
substrate in solution and Ks : half - velocity constant.
The effect of substrate concentration on the specific growth rate is shown in the figure given below ;

Growth rate can be rewritten as follows ;
 Cell Growth and Substrate Utilization...
In both batch- and continuous - growth culture systems, a portion of the substrate is converted to new cells and a portion
is oxidized to inorganic and organic end products. Because the quantity of new cells produced has been observed to be
reproducible for a given substrate, the following relationship has been developed between the rate of substrate utilization
and the rate of growth ;
Cell Growth and Substrate Utilization...
In both batch- and continuous - growth culture systems, a portion of the substrate is converted to new cells and a portion
is oxidized to inorganic and organic end products. Because the quantity of new cells produced has been observed to be
reproducible for a given substrate, the following relationship has been developed between the rate of substrate utilization
and the rate of growth ;

where ; Y : maximum yield coefficient and rsu : substrate utilization rate.
On the basis of laboratory studies, it has been concluded that yield depends on ; (1) the oxidation stage of the carbon
source and nutrient elements, (2) the degree of polymerization of the substrate, (3) pathways of metabolism, (4) the
growth rate and (5) various physical parameters of cultivation.
Substrate utilization rate can be rewritten as follows ;

The term mmax / Y is often replaced by the term k, defined as the maximum rate of substrate utilization per unit
mass of microorganisms ;

Substrate utilization rate can be rewritten as follows ;
 Effects of Endogenous Metabolism...
In bacterial systems used for wastewater treatment, the distribution of cell ages is such that not all the cells in the
system are in the log - growth phase. Consequently, the expression for the rate of growth must be corrected to account
for the energy required for cell maintenance. Other factors, such as death and predation, must also be considered. Usually,
these factors are lumped together, and it is assumed that the decrease in cell mass caused by them is proportional to the
concentration of organisms present. This decrease is often identified in the literature as the endogenous decay. The
endogenous decay term can be formulated as follows ;
Effects of Endogenous Metabolism...
In bacterial systems used for wastewater treatment, the distribution of cell ages is such that not all the cells in the
system are in the log - growth phase. Consequently, the expression for the rate of growth must be corrected to account
for the energy required for cell maintenance. Other factors, such as death and predation, must also be considered. Usually,
these factors are lumped together, and it is assumed that the decrease in cell mass caused by them is proportional to the
concentration of organisms present. This decrease is often identified in the literature as the endogenous decay. The
endogenous decay term can be formulated as follows ;

where ; kd : endogenous decay coefficient.
Net rate of growth can be obtained as follows ;


The corresponding expression for the net specific growth rate is given by equation shown below, which is the same as the
expression proposed by van Uden ;

where ; m' : net specific growth rate.
The effects of endogenous respiration on the net bacterial yield are accounted for by defining an observed yield as
follows ;
 Effects of Temperature...
The temperature dependence of the biological reaction - rate constants is very important in assessing the overall
efficiency of a biological treatment process. Temperature not only influences the metabolic activities of the microbial
population but also has a profound effect on such factors as gas - transfer rates and the settling characteristics of
the biological solids. The effect of temperature on the reaction rate of a biological process is usually expressed in the
following form ;
Effects of Temperature...
The temperature dependence of the biological reaction - rate constants is very important in assessing the overall
efficiency of a biological treatment process. Temperature not only influences the metabolic activities of the microbial
population but also has a profound effect on such factors as gas - transfer rates and the settling characteristics of
the biological solids. The effect of temperature on the reaction rate of a biological process is usually expressed in the
following form ;

where ; rT : reaction rate at T deg. C, r20 : reaction rate at 20 deg. C, theta : temperature -
activity coefficient and T : temperature.
Some typical values of theta for some commonly used biological processes are presented in table given below.
| Process |
Theta |
| Range |
Typical |
| Activated sludge |
1.00 - 1.08 |
1.04 |
| Aerated lagoons |
1.04 - 1.10 |
1.08 |
| Trickling filters |
1.02 - 1.08 |
1.04 |
Other Rate Expressions...
In reviewing the kinetic expressions used to describe the growth of microorganisms and the removal of substrate, it is
very important to remember that the expressions presented are empirical and were used for the purpose of illustration
and that they are not only expressions available. Other expressions which have been used to describe the rate of
substrate utilization include the following ;



 Microorganism and Substrate Mass Balances...
A mass balance for the mass of microorganisms in the complete - mix reactor shown below can be written as follows ;
Microorganism and Substrate Mass Balances...
A mass balance for the mass of microorganisms in the complete - mix reactor shown below can be written as follows ;



where ; dX / dt = rate of change of microorganism concentration in the reactor measured in terms of mass (VSS), Vr :
reactor volume, Q : flowrate, Xo : concentration of microorganisms in influent, X : concentration of microorganisms
in reactor (also in effluent) and rg' : net rate of microorganism growth.
If the value of rg' is substituted into the equation given above, the result is ;

If it assumed that the concentration of microorganisms in the influent can be neglected and that steady - state conditions
prevail ( dX / dt = 0), equation given above can be simplified to yield ;

where ; theta : hydraulic detention time ( V / Q ).
In equation given above, the term 1 / theta corresponds to the net specific growth rate. The term 1 / theta also corresponds
to 1 / thetac where thetac is the mean cell residence time. In the field of wastewater treatment,
thetac may be defined as the mass of organisms in the reactor divided by the mass of organisms removed from the
system each day. For the reactor shown above, thetac is given by the following expression ;

Performing a substrate balance corresponding to the microorganism mass balance results in the following expression ;

At the steady - state ( dS / dt = 0 ), the resulting equation is ;

where ; theta = Vr / Q.
Effluent Microorganism and Substrate Concentrations...
The effluent microorganisms and substrate concentrations may be obtained as follows ;


Thus, if kinetic coefficients are known, equations given just above can be used to predict effluent microorganisms and
substrate concentrations. It is important to note that the effluent concentrations predicted using the above equations
are based on a soluble waste and do not take into account any influent suspended solids that may be present. Actual
effluent substrate and suspended - solids concentrations from the treatment process are dependent on the performance of the
sedimentation tanks.
The observed yield, Yobs, is given by the following expression ;
 Process Analysis - Complete Mix with Recycle...
In the complete - mix system, shown schematically in
Process Analysis - Complete Mix with Recycle...
In the complete - mix system, shown schematically in  , the
contents of the reactor are mixed completely, and it is assumed that there are no microorganisms in the wastewater
influent. As shown in
, the
contents of the reactor are mixed completely, and it is assumed that there are no microorganisms in the wastewater
influent. As shown in  , an integral part of the activated
sludge process is a solids separation unit (sedimentation tank) in which the cells from the reactor are separated (settled)
and then returned to the reactor. Because of the presence of this solids separation unit, two additional assumptions must
be made in the development of the kinetic model for this system ;
, an integral part of the activated
sludge process is a solids separation unit (sedimentation tank) in which the cells from the reactor are separated (settled)
and then returned to the reactor. Because of the presence of this solids separation unit, two additional assumptions must
be made in the development of the kinetic model for this system ;
(1) Waste stabilization by the microorganisms occurs only in the reactor unit. This assumption leads to a conservative
model (in some systems there may be some waste stabilization in the settling unit) and (2) The volume used in calculating
the mean cell - residence time for the system includes only the volume of the reactor unit.
In effect, it is assumed that the sedimentation tank serves as a reservoir from which solids are returned to maintain a
given solids level in the aeration tank. If the system is such that these assumptions do not hold true, then the model
should be modified.
The mean hydraulic retention time for this system, thetas, is defined as ;

where ; VT : volume of reactor plus volume of settling tank, Q : influent flowrate, Vr : volume of
reactor and Vs : volume of settling tank.
The mean hydraulic retention time for the reactor, theta, is defined as ;

For the system shown in  (above), the mean cell - residence time,
thetac, defined as the mass of organisms in the reactor divided by the mass of organism removed from the system
each day, is given by the following expression ;
(above), the mean cell - residence time,
thetac, defined as the mass of organisms in the reactor divided by the mass of organism removed from the system
each day, is given by the following expression ;

where ; Qw : flowrate of liquid containing the biological cells to be removed (wasted) from the system (in this
case from the reactor), Qe : flowrate of liquid from the separation unit and Xe : microorganism
concentration in effluent from solids separation unit.
For the system shown in  (below), the mean cell - residence time,
thetac, is given by the following expression ;
(below), the mean cell - residence time,
thetac, is given by the following expression ;

where ; Xr : microorganism concentration in return sludge line and Qw' : cell wastage
rate from recycle line.
It should be noted that in the literature the value of thetac is often computed by considering the mass of
organisms in both the reactor and the sedimentation tank. Either method is acceptable as long as the basis for computation
is noted clearly. It can be seen that a given reactor volume thetac is theoretically independent of both
theta and thetas. Practically speaking, however, thetac cannot be completely independent of theta
and thetas. The factors relating thetac to theta and thetas are discussed later.
Referring to figure shown in  (above), a mass balance for the
microorganisms in the entire system can be written as follows ;
(above), a mass balance for the
microorganisms in the entire system can be written as follows ;

Substituting the rate of growth and assuming that the cell concentration in the influent is zero and steady - state
conditions prevail ( dX / dt = 0 ) yields ;

The left - hand side of the equation given just above represents the inverse of the mean cell - residence time as defined
previously. Thetac can be rearranged as follows ;

The term rsu is determined using the following expression ;

The mass concentration of microorganisms, X, in the reactor can be obtained by ;

Performing a substrate balance, the effluent substrate concentration is found to be equal to ;

The corresponding equation for the observed yield in a system with recycle is ;
 Process Design and Control Relationships...
Although equations given just above can be useful in predicting the effects of various system changes, they are somewhat
difficult to use from a design standpoint because of the many constants involved. For this reason, more usable process
design relationships have been developed. The relationships to be considered in the following discussion include the
specific utilization rate, mean cell - residence time, and the food - microorganism ratio. The relationship between the
specific utilization rate and the mean cell - residence time is also examined.
Process Design and Control Relationships...
Although equations given just above can be useful in predicting the effects of various system changes, they are somewhat
difficult to use from a design standpoint because of the many constants involved. For this reason, more usable process
design relationships have been developed. The relationships to be considered in the following discussion include the
specific utilization rate, mean cell - residence time, and the food - microorganism ratio. The relationship between the
specific utilization rate and the mean cell - residence time is also examined.
The term ( - rsu / X ) is known as the specific substrate utilization rate, U. Using the definition of
rsu, the specific utilization rate is calculated as follows ;

If the term U is substituted for the term ( - rsu / X ), the resulting equation is ;

It can be seen that 1 / thetac, the net specific growth rate, and U, the specific utilization ratio, are
related directly. To determine the specific utilization ratio, U, the substrate utilized and the mass of microorganisms
effective in this utilization must be known. The substrate utilized can be evaluated by determining the difference
between the influent and the effluent COD or BOD5. The evaluation of the active mass of microorganisms is
usually what makes the use of U impractical as a control parameter.
Using thetac as a treatment control parameter, there is neither the need to determine the amount of active
biological solids in the system nor the need to evaluate the amount of food utilized. The use of thetac is
simply based on the fact that, to control the growth rate of microorganisms and hence their degree of waste stabilization,
a specified percentage of the cell mass in the system must be wasted each day. Thus, if it is determined that a thetac
of 10 days is needed for a desired treatment efficiency, then 10 percent of the total cell mass is wasted from the system
per day.
In the complete - mix system with recycle, cell wastage can be accomplished by wasting from the reactor of mixed - liquor
return line. If wasting is directly from the reactor and the solids in the effluent Xe are negligible then
only Qw and Vr need to be known to determine thetac. Wasting cells in this manner provides
for a direct method of controlling and measuring thetac. In practice, to obtain a thicker sludge, wasting is
accomplished by drawing off sludge from the recycle line. Assuming that Xe is very small, thetac can
be rewritten as ;

Thus, wasting from the recycle line requires that the microorganism concentrations in both the mixed liquor and return
sludge be known.
A term closely related to the specific utilization rate, U, and commonly used in practice as a design and control parameter
is known as the food - microorganism ratio ( F / M ), which is defined as follows ;

The terms U and F / M are related by the process efficiency as follows ;

where ; E : is the process efficiency ;




 "Schematic of Complete - Mix Reactor"...
"Schematic of Complete - Mix Reactor"...
 "Schematic of Complete - Mix Reactor"...
"Schematic of Complete - Mix Reactor"...































 , the
contents of the reactor are mixed completely, and it is assumed that there are no microorganisms in the wastewater
influent. As shown in
, the
contents of the reactor are mixed completely, and it is assumed that there are no microorganisms in the wastewater
influent. As shown in  , an integral part of the activated
sludge process is a solids separation unit (sedimentation tank) in which the cells from the reactor are separated (settled)
and then returned to the reactor. Because of the presence of this solids separation unit, two additional assumptions must
be made in the development of the kinetic model for this system ;
, an integral part of the activated
sludge process is a solids separation unit (sedimentation tank) in which the cells from the reactor are separated (settled)
and then returned to the reactor. Because of the presence of this solids separation unit, two additional assumptions must
be made in the development of the kinetic model for this system ;

 (above), the mean cell - residence time,
thetac, defined as the mass of organisms in the reactor divided by the mass of organism removed from the system
each day, is given by the following expression ;
(above), the mean cell - residence time,
thetac, defined as the mass of organisms in the reactor divided by the mass of organism removed from the system
each day, is given by the following expression ;
 (below), the mean cell - residence time,
thetac, is given by the following expression ;
(below), the mean cell - residence time,
thetac, is given by the following expression ;
 (above), a mass balance for the
microorganisms in the entire system can be written as follows ;
(above), a mass balance for the
microorganisms in the entire system can be written as follows ;














