Release 9.2
Part No. A96630-01
Library |
Product |
Contents |
 Master Index |
Index |
 Feedback |
| Oracle® Spatial User's Guide and Reference Release 9.2 Part No. A96630-01 |
|
Oracle Spatial is an integrated set of functions and procedures that enables spatial data to be stored, accessed, and analyzed quickly and efficiently in an Oracle9i database.
Spatial data represents the essential location characteristics of real or conceptual objects as those objects relate to the real or conceptual space in which they exist.
Oracle Spatial, often referred to as Spatial, provides a SQL schema and functions that facilitate the storage, retrieval, update, and query of collections of spatial features in an Oracle9i database. Spatial consists of the following components:
A schema (MDSYS) that prescribes the storage, syntax, and semantics of supported geometric data types
A spatial indexing mechanism
A set of operators and functions for performing area-of-interest queries, spatial join queries, and other spatial analysis operations
Administrative utilities
The spatial component of a spatial feature is the geometric representation of its shape in some coordinate space. This is referred to as its geometry.
Spatial supports the object-relational model for representing geometries. The object-relational model uses a table with a single column of MDSYS.SDO_GEOMETRY and a single row per geometry instance. The object-relational model corresponds to a "SQL with Geometry Types" implementation of spatial feature tables in the OpenGIS ODBC/SQL specification for geospatial features.
|
Note: The relational geometry model of Oracle Spatial is no longer supported, effective with this release. Only the object-relational model is supported. |
The benefits provided by the object-relational model include:
Support for many geometry types, including arcs, circles, compound polygons, compound line strings, and optimized rectangles
Ease of use in creating and maintaining indexes and in performing spatial queries
Index maintenance by the Oracle9i database server
Geometries modeled in a single row and single column
Optimal performance
Oracle Spatial is designed to make spatial data management easier and more natural to users of location-enabled applications and Geographic Information System (GIS) applications. Once this data is stored in an Oracle database, it can be easily manipulated, retrieved, and related to all the other data stored in the database.
A common example of spatial data can be seen in a road map. A road map is a two-dimensional object that contains points, lines, and polygons that can represent cities, roads, and political boundaries such as states or provinces. A road map is a visualization of geographic information. The location of cities, roads, and political boundaries that exist on the surface of the Earth are projected onto a two-dimensional display or piece of paper, preserving the relative positions and relative distances of the rendered objects.
The data that indicates the Earth location (latitude and longitude, or height and depth) of these rendered objects is the spatial data. When the map is rendered, this spatial data is used to project the locations of the objects on a two-dimensional piece of paper. A GIS is often used to store, retrieve, and render this Earth-relative spatial data.
Types of spatial data that can be stored using Spatial other than GIS data include data from computer-aided design (CAD) and computer-aided manufacturing (CAM) systems. Instead of operating on objects on a geographic scale, CAD/CAM systems work on a smaller scale, such as for an automobile engine or printed circuit boards.
The differences among these systems are only in the relative sizes of the data, not the data's complexity. The systems might all actually involve the same number of data points. On a geographic scale, the location of a bridge can vary by a few tenths of an inch without causing any noticeable problems to the road builders, whereas if the diameter of an engine's pistons are off by a few tenths of an inch, the engine will not run. A printed circuit board is likely to have many thousands of objects etched on its surface that are no bigger than the smallest detail shown on a road builder's blueprints.
These applications all store, retrieve, update, or query some collection of features that have both nonspatial and spatial attributes. Examples of nonspatial attributes are name, soil_type, landuse_classification, and part_number. The spatial attribute is a coordinate geometry, or vector-based representation of the shape of the feature.
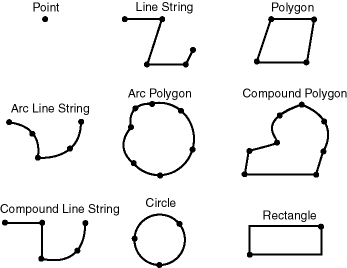
A geometry is an ordered sequence of vertices that are connected by straight line segments or circular arcs. The semantics of the geometry are determined by its type. Spatial supports several primitive types and geometries composed of collections of these types, including two-dimensional:
Points and point clusters
Line strings
n-point polygons
Arc line strings (All arcs are generated as circular arcs.)
Arc polygons
Compound polygons
Compound line strings
Circles
Optimized rectangles
Two-dimensional points are elements composed of two ordinates, X and Y, often corresponding to longitude and latitude. Line strings are composed of one or more pairs of points that define line segments. Polygons are composed of connected line strings that form a closed ring and the area of the polygon is implied.
Self-crossing polygons are not supported, although self-crossing line strings are supported. If a line string crosses itself, it does not become a polygon. A self-crossing line string does not have any implied area.
Figure 1-1 illustrates the geometric types.
Figure 1-1 Geometric Types
Spatial also supports the storage and indexing of three-dimensional and four-dimensional geometric types, where three or four coordinates are used to define each vertex of the object being defined. However, spatial functions (except for LRS functions and MBR-related functions) can work with only the first two dimensions, and all spatial operators except SDO_FILTER are disabled if the spatial index has been created on more than two dimensions.
The Spatial data model is a hierarchical structure consisting of elements, geometries, and layers, which correspond to representations of spatial data. Layers are composed of geometries, which in turn are made up of elements.
For example, a point might represent a building location, a line string might represent a road or flight path, and a polygon might represent a state, city, zoning district, or city block.
An element is the basic building block of a geometry. The supported spatial element types are points, line strings, and polygons. For example, elements might model star constellations (point clusters), roads (line strings), and county boundaries (polygons). Each coordinate in an element is stored as an X,Y pair. The exterior ring and the interior ring of a polygon with holes are considered as two distinct elements that together make up a complex polygon.
Point data consists of one coordinate. Line data consists of two coordinates representing a line segment of the element. Polygon data consists of coordinate pair values, one vertex pair for each line segment of the polygon. Coordinates are defined in order around the polygon (counterclockwise for an exterior polygon ring, clockwise for an interior polygon ring).
A geometry (or geometry object) is the representation of a spatial feature, modeled as an ordered set of primitive elements. A geometry can consist of a single element, which is an instance of one of the supported primitive types, or a homogeneous or heterogeneous collection of elements. A multipolygon, such as one used to represent a set of islands, is a homogeneous collection. A heterogeneous collection is one in which the elements are of different types, for example, a point and a polygon.
An example of a geometry might describe the buildable land in a town. This could be represented as a polygon with holes where water or zoning prevents construction.
A layer is a collection of geometries having the same attribute set. For example, one layer in a GIS might include topographical features, while another describes population density, and a third describes the network of roads and bridges in the area (lines and points). Each layer's geometries and associated spatial index are stored in the database in standard tables.
A coordinate system (also called a spatial reference system) is a means of assigning coordinates to a location and establishing relationships between sets of such coordinates. It enables the interpretation of a set of coordinates as a representation of a position in a real world space.
Any spatial data has a coordinate system associated with it. The coordinate system can be georeferenced (related to a specific representation of the Earth) or not georeferenced (that is, Cartesian, and not related to a specific representation of the Earth). If the coordinate system is georeferenced, it has a default unit of measurement (such as meters) associated with it, but you can have Spatial automatically return results in another specified unit (such as miles). (For more information about unit of measurement support, see Section 2.6.)
Before Oracle Spatial release 8.1.6, geometries (objects of type SDO_GEOMETRY) were stored as strings of coordinates without reference to any specific coordinate system. Spatial functions and operators always assumed a coordinate system that had the properties of an orthogonal Cartesian system, and sometimes did not provide correct results if Earth-based geometries were stored in latitude and longitude coordinates. With release 8.1.6, Spatial provided support for many different coordinate systems, and for converting data freely between different coordinate systems.
Spatial data can be associated with a Cartesian, geodetic (geographical), projected, or local coordinate system:
Cartesian coordinates are coordinates that measure the position of a point from a defined origin along axes that are perpendicular in the represented two-dimensional or three-dimensional space.
If a coordinate system is not explicitly associated with a geometry, a Cartesian coordinate system is assumed.
Geodetic coordinates (sometimes called geographic coordinates) are angular coordinates (longitude and latitude), closely related to spherical polar coordinates, and are defined relative to a particular Earth geodetic datum. (A geodetic datum is a means of representing the figure of the Earth and is the reference for the system of geodetic coordinates.)
Projected coordinates are planar Cartesian coordinates that result from performing a mathematical mapping from a point on the Earth's surface to a plane. There are many such mathematical mappings, each used for a particular purpose.
Local coordinates are Cartesian coordinates in a non-Earth (non-georeferenced) coordinate system. Local coordinate systems are often used for CAD applications and local surveys.
When performing operations on geometries, Spatial uses either a Cartesian or curvilinear computational model, as appropriate for the coordinate system associated with the spatial data.
For more information about coordinate system support in Spatial, including geodetic, projected, and local coordinates and coordinate system transformation, see Chapter 5.
Tolerance is used to associate a level of precision with spatial data. Tolerance reflects the distance that two points can be apart and still be considered the same (for example, to accommodate rounding errors). The tolerance value must be a non-negative number greater than zero. The significance of the value depends on whether or not the spatial data is associated with a geodetic coordinate system. (Geodetic and other types of coordinate systems are described in Section 1.5.4.)
For geodetic data (such as data identified by longitude and latitude coordinates), the tolerance value is a number of meters. For example, a tolerance value of 100 indicates a tolerance of 100 meters.
For non-geodetic data, the tolerance value is a number of the units that are associated with the coordinate system associated with the data. For example, if the unit of measurement is miles, a tolerance value of 0.005 indicates a tolerance of 0.005 (that is, 1/200) mile (approximately 105 feet), and a tolerance value of 2 indicates a tolerance of two miles.
In both cases, the smaller the tolerance value, the more precision is to be associated with the data.
A tolerance value is specified in two cases:
In the geometry metadata definition for a layer (see Section 1.5.5.1)
As an optional input parameter to certain functions (see Section 1.5.5.2)
The dimensional information for a layer includes a tolerance value. Specifically, the DIMINFO column (described in Section 2.4.3) of the xxx_SDO_GEOM_METADATA views includes an SDO_TOLERANCE value.
If a function accepts an optional tolerance parameter and this parameter is null or not specified, the SDO_TOLERANCE value of the layer is used. Using the non-geodetic data from the example in Section 2.1, the actual distance between geometries cola_b and cola_d is 0.846049894. If a query uses the SDO_GEOM.SDO_DISTANCE function to return the distance between cola_b and cola_d and does not specify a tolerance parameter value, the result depends on the SDO_TOLERANCE value of the layer. For example:
If the SDO_TOLERANCE value of the layer is 0.005, this query returns .846049894.
If the SDO_TOLERANCE value of the layer is 0.5, this query returns 0.
The zero result occurs because Spatial first constructs an imaginary buffer of the tolerance value (0.5) around each geometry to be considered, and the buffers around cola_b and cola_d overlap in this case.
You can therefore take either of two approaches in selecting an SDO_TOLERANCE value for a layer:
The value can reflect the desired level of precision in queries for distances between objects. For example, if two non-geodetic geometries 0.8 units apart should be considered as separated, specify a small SDO_TOLERANCE value such as 0.05 or smaller.
The value can reflect the precision of the values associated with geometries in the layer. For example, if all the geometries in a non-geodetic layer are defined using integers and if two objects 0.8 units apart should not be considered as separated, an SDO_TOLERANCE value of 0.5 is appropriate. To have greater precision in any query, you must override the default by specifying the tolerance parameter.
With non-geodetic data, the guideline to follow for most instances of the second case (precision of the values of the geometries in the layer) is: take the highest level of precision in the geometry definitions, and use .5 at the next level as the SDO_TOLERANCE value. For example, if geometries are defined using integers (as in the simplified example in Section 2.1), the appropriate value is 0.5. However, if geometries are defined using numbers up to 4 decimal positions (for example, 31.2587), such as with longitude and latitude values, the appropriate value is 0.00005.
|
Note: This guideline, however, should not be used if the geometries include any polygons that are so narrow at any point that the distance between facing sides is less than the proposed tolerance value. Be sure that the tolerance value is less than the shortest distance between any two sides in any polygon.Moreover, if you encounter "invalid geometry" errors with inserted or updated geometries, and if the geometries are in fact valid, consider increasing the precision of the tolerance value (for example, changing 0.00005 to 0.000005). |
Many Spatial functions accept an optional tolerance parameter, which (if specified) overrides the default tolerance value for the layer (explained in Section 1.5.5.1). If the distance between two points is less than or equal to the tolerance value, Spatial considers the two points to be a single point. Thus, tolerance is usually a reflection of how accurate or precise users perceive their spatial data to be.
For example, assume that you want to know which restaurants are within 5 kilometers of your house. Assume also that Maria's Pizzeria is 5.1 kilometers from your house. If the spatial data has a geodetic coordinate system and if you ask, Find all restaurants within 5 kilometers and use a tolerance of 100 (or greater, such as 500), Maria's Pizzeria will be included, because 5.1 kilometers (5100 meters) is within 100 meters of 5 kilometers (5000 meters). However, if you specify a tolerance less than 100 (such as 50), Maria's Pizzeria will not be included.
Tolerance values for Spatial functions are typically very small, although the best value in each case depends on the kinds of applications that use or will use the data.
Spatial uses a two-tier query model to resolve spatial queries and spatial joins. The term is used to indicate that two distinct operations are performed to resolve queries. The output of the two combined operations yields the exact result set.
The two operations are referred to as primary and secondary filter operations.
The primary filter permits fast selection of candidate records to pass along to the secondary filter. The primary filter compares geometry approximations to reduce computation complexity and is considered a lower-cost filter. Because the primary filter compares geometric approximations, it returns a superset of the exact result set.
The secondary filter applies exact computations to geometries that result from the primary filter. The secondary filter yields an accurate answer to a spatial query. The secondary filter operation is computationally expensive, but it is only applied to the primary filter results, not the entire data set.
Figure 1-2 illustrates the relationship between the primary and secondary filters.
Figure 1-2 Query Model
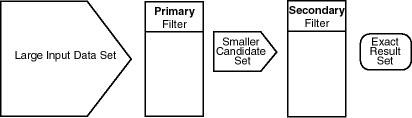
As shown in Figure 1-2, the primary filter operation on a large input data set produces a smaller candidate set, which contains at least the exact result set and may contain more records. The secondary filter operation on the smaller candidate set produces the exact result set.
Spatial uses a spatial index to implement the primary filter. Spatial does not require the use of both the primary and secondary filters. In some cases, just using the primary filter is sufficient. For example, a zoom feature in a mapping application queries for data that has any interaction with a rectangle representing visible boundaries. The primary filter very quickly returns a superset of the query. The mapping application can then apply clipping routines to display the target area.
The purpose of the primary filter is to quickly create a subset of the data and reduce the processing burden on the secondary filter. The primary filter therefore should be as efficient (that is, selective yet fast) as possible. This is determined by the characteristics of the spatial index on the data.
For more information about querying spatial data, see Section 4.2.
The introduction of spatial indexing capabilities into the Oracle database engine is a key feature of the Spatial product. A spatial index, like any other index, provides a mechanism to limit searches, but in this case based on spatial criteria such as intersection and containment. A spatial index is needed to:
Find objects within an indexed data space that interact with a given point or area of interest (window query)
Find pairs of objects from within two indexed data spaces that interact spatially with each other (spatial join)
A spatial index is considered a logical index. The entries in the spatial index are dependent on the location of the geometries in a coordinate space, but the index values are in a different domain. Index entries may be ordered using a linearly ordered domain, and the coordinates for a geometry may be pairs of integer, floating-point, or double-precision numbers.
Oracle Spatial lets you use R-tree indexing (the default) or quadtree indexing, or both. Each index type is appropriate in different situations. You can maintain both an R-tree and quadtree index on the same geometry column, by using the add_index parameter with the ALTER INDEX statement (described in Chapter 8), and you can choose which index to use for a query by specifying the idxtab1 and/or idxtab2 parameters with certain Spatial operators, such as SDO_RELATE, described in Chapter 10.
In choosing whether to use an R-tree or quadtree index for a spatial application, consider the items in Table 1-1.
Table 1-1 Choosing R-tree or Quadtree Indexing
| R-tree Indexing | Quadtree Indexing |
|---|---|
| The approximation of geometries cannot be fine-tuned. (Spatial uses the minimum bounding rectangles, as described in Section 1.7.1.) | The approximation of geometries can be fine-tuned by setting the tiling level and number of tiles. |
| Index creation and tuning are easier. | Tuning is more complex, and setting the appropriate tuning parameter values can affect performance significantly. |
| Less storage is required. | More storage is required. |
| If your application workload includes nearest-neighbor queries (SDO_NN operator), R-tree indexes are faster. | If your application workload includes nearest-neighbor queries (SDO_NN operator), quadtree indexes are slower. |
| If there is heavy update activity to the spatial column, an R-tree index may not be a good choice. | Heavy update activity does not affect the performance of a quadtree index. |
| You can index up to four dimensions. | You can index only two dimensions. |
| An R-tree index is recommended for indexing geodetic data if SDO_WITHIN_DISTANCE queries will be used on it. | |
| An R-tree index is required for a whole-earth index. |
Testing of R-tree and quadtree indexes with many workloads and operators is ongoing, and results and recommendations will be documented as they become available. However, before choosing an index type for an application, you should understand the concepts and options associated with both R-tree indexing (described in Section 1.7.1) and quadtree indexing (described in Section 1.7.2).
A spatial R-tree index can index spatial data of up to four dimensions. An R-tree index approximates each geometry by a single rectangle that minimally encloses the geometry (called the minimum bounding rectangle, or MBR), as shown in Figure 1-3.
Figure 1-3 MBR Enclosing a Geometry
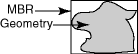
For a layer of geometries, an R-tree index consists of a hierarchical index on the MBRs of the geometries in the layer, as shown in Figure 1-4.
Figure 1-4 R-tree Hierarchical Index on MBRs
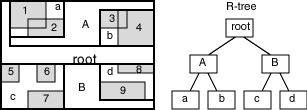
In Figure 1-4:
1 through 9 are geometries in a layer.
a, b, c, and d are the leaf nodes of the R-tree index, and contain minimum bounding rectangles of geometries, along with pointers to the geometries. For example, a contains the MBR of geometries 1 and 2, b contains the MBR of geometries 3 and 4, and so on.
A contains the MBR of a and b, and B contains the MBR of c and d.
The root contains the MBR of A and B (that is, the entire area shown).
An R-tree index is stored in the spatial index table (SDO_INDEX_TABLE in the USER_SDO_INDEX_METADATA view, described in Section 2.5). The R-tree index also maintains a sequence number generator (SDO_RTREE_SEQ_NAME in the USER_SDO_INDEX_METADATA view) to ensure that simultaneous updates by concurrent users can be made to the index.
A substantial number of insert and delete operations affecting an R-tree index may degrade the quality of the R-tree structure, which may adversely affect query performance.
The R-tree is a hierarchical tree structure with nodes at different heights of the tree. The performance of an R-tree index structure for queries is roughly proportional to the area and perimeter of the index nodes of the R-tree. The area covered at level 0 represents the area occupied by the minimum bounding rectangles of the data geometries, the area at level 1 indicates the area covered by leaf-level R-tree nodes, and so on. The original ratio of the area at the root (topmost level) to the area at level 0 can change over time based on updates to the table; and if there is a degradation in that ratio (that is, if it increases significantly), rebuilding the index may help the performance of queries.
Spatial provides several functions and procedures related to the quality of an R-tree index:
SDO_TUNE.ANALYZE_RTREE provides advice about whether or not an index needs to be rebuilt. It computes the current index quality score and compares it to the quality score when the index was created or most recently rebuilt, and it displays a recommendation.
SDO_TUNE.RTREE_QUALITY returns the current index quality score.
SDO_TUNE.QUALITY_DEGRADATION returns the current index quality degradation.
These functions and procedures are described in Chapter 16.
To rebuild an R-tree index, use the ALTER INDEX REBUILD statement, which is described in Chapter 8.
In the linear quadtree indexing scheme, the coordinate space (for the layer where all geometric objects are located) is subjected to a process called tessellation, which defines exclusive and exhaustive cover tiles for every stored geometry. Tessellation is done by decomposing the coordinate space in a regular hierarchical manner. The range of coordinates, the coordinate space, is viewed as a rectangle. At the first level of decomposition, the rectangle is divided into halves along each coordinate dimension generating four tiles. Each tile that interacts with the geometry being tessellated is further decomposed into four tiles. This process continues until some termination criteria, such as size of the tiles or the maximum number of tiles to cover the geometry, is met.
Spatial can use either fixed-size or variable-sized tiles to cover a geometry:
Fixed-size tiles are controlled by tile resolution. If the resolution is the sole controlling factor, then tessellation terminates when the coordinate space has been decomposed a specific number of times. Therefore, each tile is of a fixed size and shape.
Variable-sized tiling is controlled by the value supplied for the maximum number of tiles. If the number of tiles per geometry, n, is the sole controlling factor, the tessellation terminates when n tiles have been used to cover the given geometry.
Fixed-size tile resolution and the number of variable-sized tiles used to cover a geometry are user-selectable parameters called SDO_LEVEL and SDO_NUMTILES, respectively. Smaller fixed-size tiles or more variable-sized tiles provides better geometry approximations. The smaller the number of tiles, or the larger the tiles, the coarser are the approximations.
Spatial supports two quadtree indexing types, reflecting two valid combinations of SDO_LEVEL and SDO_NUMTILES values:
Fixed indexing: a non-null and non-zero SDO_LEVEL value and a null or zero (0) SDO_NUMTILES value, resulting in fixed-sized tiles. Fixed indexing is described in Section 1.7.2.2.
Hybrid indexing: non-null and non-zero values for SDO_LEVEL and SDO_NUMTILES, resulting in two sets of tiles per geometry. One set contains fixed-size tiles and the other set contains variable-sized tiles. Hybrid indexing is not recommended for most spatial applications, and is described in Appendix B.
The process of determining which tiles cover a given geometry is called tessellation. The tessellation process is a quadtree decomposition, where the two-dimensional coordinate space is broken down into four covering tiles of equal size. Successive tessellations divide those tiles that interact with the geometry down into smaller tiles, and this process continues until the desired level or number of tiles has been achieved. The results of the tessellation process on a geometry are stored in a table, referred to as the SDOINDEX table.
The tiles at a particular level can be linearly sorted by systematically visiting tiles in an order determined by a space-filling curve as shown in Figure 1-5. The tiles can also be assigned unique numeric identifiers, known as Morton codes or z-values. The terms tile and tile code will be used interchangeably in this and other sections related to spatial indexing.
Figure 1-5 Quadtree Decomposition and Morton Codes
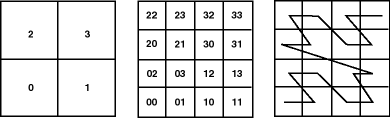
Fixed spatial indexing uses tiles of equal size to cover a geometry. Because all the tiles are the same size, they all have codes of the same length, and the standard SQL equality operator (=) can be used to compare tiles during a join operation. This results in excellent performance characteristics.
Two geometries are likely to interact, and hence pass the primary filter stage, if they share one or more tiles. The SQL statement for the primary filter stage is:
SELECT DISTINCT <select_list for geometry identifiers>
FROM table1_sdoindex A, table2_sdoindex B
WHERE A.sdo_code = B.sdo_code
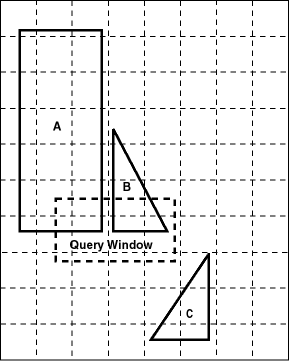
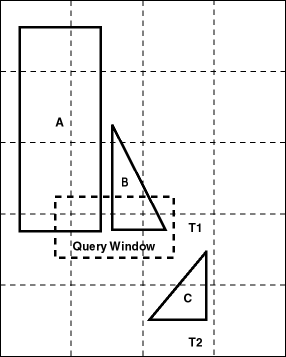
The effectiveness and efficiency of this indexing method depends on the tiling level and the variation in size of the geometries in the layer. If you select a small fixed-size tile to cover small geometries and then try to use the same size tile to cover a very large geometry, a large number of tiles would be required. However, if the chosen tile size is large, so that fewer tiles are generated in the case of a large geometry, then the index selectivity suffers because the large tiles do not approximate the small geometries very well. Figure 1-6 and Figure 1-7 illustrate the relationships between tile size, selectivity, and the number of cover tiles.
With a small fixed-size tile as shown in Figure 1-6, selectivity is good, but a large number of tiles is needed to cover large geometries. A window query would easily identify geometries A and B, but would reject C.
Figure 1-6 Fixed-Size Tiling with Many Small Tiles
With a large fixed-size tile as shown in Figure 1-7, fewer tiles are needed to cover the geometries, but the selectivity is not as good. The same window query as in Figure 1-6 would probably pick up all three geometries. Any object that shares tile T1 or T2 would identify object C as a candidate, even though the objects may be far apart, such as objects B and C are in Figure 1-7.
Figure 1-7 Fixed-Size Tiling with Fewer Large Tiles
You can use the SDO_TUNE.ESTIMATE_TILING_LEVEL function or the tiling wizard of the Spatial Index Advisor tool in Oracle Enterprise Manager to help determine an appropriate tiling level for your data set.
Figure 1-8 illustrates geometry 1013 tessellated to three fixed-sized tiles at level 1. The codes for these cover tiles are then stored in an SDOINDEX table.
Figure 1-8 Tessellated Geometry
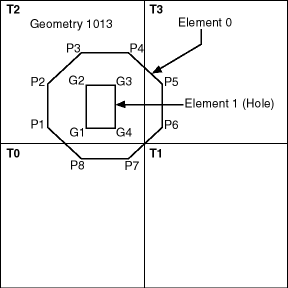
Only three of the four tiles generated by the first tessellation interact with the geometry. Only those tiles that interact with the geometry are stored in the SDOINDEX table, as shown in Table 1-2. In this example, three fixed-size tiles are used. The table structure is shown for illustrative purposes only, because you should not directly access the index tables.
Table 1-2 SDOINDEX Table Using Fixed-Size Tiles
| SDO_GID <number> | SDO_CODE <raw> |
|---|---|
| 1013 | T0 |
| 1013 | T2 |
| 1013 | T3 |
All elements in a geometry are tessellated. In a multielement geometry such as 1013, Element 1 is already covered by tile T2 from the tessellation of Element 0. If, however, the specified tiling resolution was such that tile T2 was further subdivided and one of these smaller tiles was completely contained in Element 1, then that tile would be excluded because it would not interact with the geometry.
Spatial uses secondary filters to determine the spatial relationship between entities in the database. The spatial relation is based on geometry locations. The most common spatial relations are based on topology and distance. For example, the boundary of an area consists of a set of curves that separates the area from the rest of the coordinate space. The interior of an area consists of all points in the area that are not on its boundary. Given this, two areas are said to be adjacent if they share part of a boundary but do not share any points in their interior.
The distance between two spatial objects is the minimum distance between any points in them. Two objects are said to be within a given distance of one another if their distance is less than the given distance.
To determine spatial relations, Spatial has several secondary filter methods:
The SDO_RELATE operator evaluates topological criteria.
The SDO_WITHIN_DISTANCE operator determines if two spatial objects are within a specified distance of each other.
The SDO_NN operator identifies the nearest neighbors for a spatial object.
The syntax of these operators is given in Chapter 10.
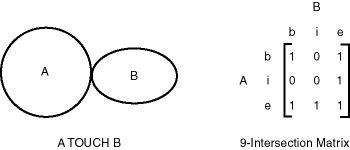
The SDO_RELATE operator implements a 9-intersection model for categorizing binary topological relations between points, lines, and polygons. Each spatial object has an interior, a boundary, and an exterior. The boundary consists of points or lines that separate the interior from the exterior. The boundary of a line consists of its end points. The boundary of a polygon is the line that describes its perimeter. The interior consists of points that are in the object but not on its boundary, and the exterior consists of those points that are not in the object.
Given that an object A has 3 components (a boundary Ab, an interior Ai, and an exterior Ae), any pair of objects has 9 possible interactions between their components. Pairs of components have an empty (0) or a non-empty (1) set intersection. The set of interactions between 2 geometries is represented by a 9-intersection matrix that specifies which pairs of components intersect and which do not. Figure 1-9 shows the 9-intersection matrix for 2 polygons that are adjacent to one another. This matrix yields the following bit mask, generated in row-major form: Ò101001111Ó.
Figure 1-9 The 9-Intersection Model
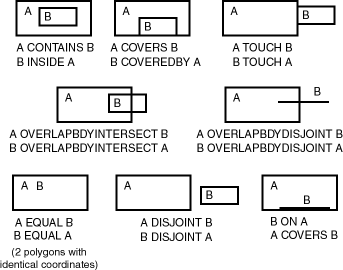
Some of the topological relationships identified in the seminal work by Professor Max Egenhofer (University of Maine, Orono) and colleagues have names associated with them. Spatial uses the following names:
DISJOINT -- The boundaries and interiors do not intersect.
TOUCH -- The boundaries intersect but the interiors do not intersect.
OVERLAPBDYDISJOINT -- The interior of one object intersects the boundary and interior of the other object, but the two boundaries do not intersect. This relationship occurs, for example, when a line originates outside a polygon and ends inside that polygon.
OVERLAPBDYINTERSECT -- The boundaries and interiors of the two objects intersect.
EQUAL -- The two objects have the same boundary and interior.
CONTAINS -- The interior and boundary of one object is completely contained in the interior of the other object.
COVERS -- The interior of one object is completely contained in the interior of the other object and their boundaries intersect.
INSIDE -- The opposite of CONTAINS. A INSIDE B implies B CONTAINS A.
COVEREDBY -- The opposite of COVERS. A COVEREDBY B implies B COVERS A.
ON -- The interior and boundary of one object is on the boundary of the other object (and the second object covers the first object). This relationship occurs, for example, when a line is on the boundary of a polygon.
ANYINTERACT -- The objects are non-disjoint.
Figure 1-10 illustrates these topological relationships.
Figure 1-10 Topological Relationships
The SDO_WITHIN_DISTANCE operator determines if two spatial objects, A and B, are within a specified distance of one another. This operator first constructs a distance buffer, Db, around the reference object B. It then checks that A and Db are non-disjoint. The distance buffer of an object consists of all points within the given distance from that object. Figure 1-11 shows the distance buffers for a point, a line, and a polygon.
Figure 1-11 Distance Buffers for Points, Lines, and Polygons
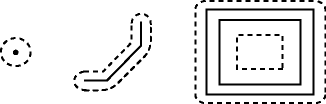
In the geometries shown in Figure 1-11:
The dashed lines represent distance buffers. Notice how the buffer is rounded near the corners of the objects.
The geometry on the right is a polygon with a hole: the large rectangle is the exterior polygon ring and the small rectangle is the interior polygon ring (the hole). The dashed line outside the large rectangle is the buffer for the exterior ring, and the dashed line inside the small rectangle is the buffer for the interior ring.
The SDO_NN operator returns a specified number of objects from a geometry column that are closest to a specified geometry (for example, the five closest restaurants to a city park). In determining how close two geometry objects are, the shortest possible distance between any two points on the surface of each object is used.
SQL has long had aggregate functions, which are used to aggregate the results of a SQL query. The following example uses the SUM aggregate function to aggregate employee salaries by department:
SELECT SUM(salary), dept FROM employees GROUP BY dept;
Oracle Spatial aggregate functions aggregate the results of SQL queries involving geometry objects. Spatial aggregate functions return a geometry object of type SDO_GEOMETRY. For example, the following statement returns the minimum bounding rectangle of all the geometries in a table (using the definitions and data from Section 2.1):
SELECT SDO_AGGR_MBR(shape) FROM cola_markets;
The following example returns the union of all geometries except cola_d:
SELECT SDO_AGGR_UNION(MDSYS.SDOAGGRTYPE(c.shape, 0.005)) FROM cola_markets c WHERE c.name < 'cola_d';
All geometries used with spatial aggregate functions must be defined using 4-digit SDO_GTYPE values (that is, must be in the format used by Oracle Spatial release 8.1.6 or higher). For information about SDO_GTYPE values, see Section 2.2.1.
For reference information about the spatial aggregate functions and examples of their use, see Chapter 12.
Many spatial aggregate functions accept an input parameter of type MDSYS.SDOAGGRTYPE. Oracle Spatial defines the object type SDOAGGRTYPE as:
CREATE TYPE sdoaggrtype AS OBJECT ( geometry MDSYS.SDO_GEOMETRY, tolerance NUMBER);
|
Note: Do not use SDOAGGRTYPE as the data type for a column in a table. Use this type only in calls to spatial aggregate functions. |
The tolerance value in the SDOAGGRTYPE definition should be the same as the SDO_TOLERANCE value specified in the DIMINFO in the xxx_SDO_GEOM_METADATA views for the geometries, unless you have a specific reason for wanting a different value. For more information about tolerance, see Section 1.5.5; for information about the xxx_SDO_GEOM_METADATA views, see Section 2.4.
The tolerance value in the SDOAGGRTYPE definition can affect the result of a spatial aggregate function. Figure 1-12 shows a spatial aggregate union (SDO_AGGR_UNION) operation of two geometries using two different tolerance values: one smaller and one larger than the distance between the geometries.
Figure 1-12 Tolerance in an Aggregate Union Operation
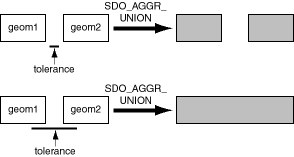
In the first aggregate union operation in Figure 1-12, where the tolerance is less than the distance between the rectangles, the result is a compound geometry consisting of two rectangles. In the second aggregate union operation, where the tolerance is greater than the distance between the rectangles, the result is a single geometry.
Geocoding is the process of converting tables of address data into standardized address, location, and possibly other data. The result of a geocoding operation is the pair of longitude and latitude coordinates that correspond with the input address or location. For example, if the input address is 22 Monument Square, Concord, MA 01742, the result of the geocoding operation is -71.34937, 42.46101.
Given a geocoded address, you can then perform proximity or location queries using a spatial engine, such as Oracle Spatial, or demographic analysis using tools and data from Oracle's business partners. In addition, geocoded data can be used with other spatial data such as block group, postal code, and county code for association with demographic information. Results of analyses or queries can be presented as maps, in addition to tabular formats, using third-party software integrated with Oracle Spatial.
Oracle Spatial is integrated with all major geocoding service providers. The usual and recommended approach for application developers is to use the API for the geocoding provider to obtain a geocoded result (longitude/latitude coordinate pair) for an address, and then use these coordinates to construct an MDSYS.SDO_GEOMETRY object for input to a spatial operator, function, or procedure.
Many factors can affect the performance of Oracle Spatial applications, such as the indexing method (R-tree or quadtree), the SOD_LEVEL value for a quadtree index, and the use of optimizer hints to influence the plan for query execution. This guide contains some information about performance and tuning where it is relevant to a particular topic. For example, Section 1.7 includes performance-related items among the considerations for choosing an R-tree or quadtree index.
In addition, more Spatial performance and tuning information is available in one or more white papers through the Oracle Technology Network (OTN). That information is often more detailed than what is in this guide, and it is periodically updated as a result of internal testing and consultations with Spatial users. To find that information on the OTN, go to
Search for Spatial, and then search for white papers relevant to performance and tuning.
To check which release of Spatial you are running, use the SDO_VERSION function. For example:
SELECT SDO_VERSION FROM DUAL; SDO_VERSION -------------------------------------------------------------------------------- 9.0.1
The SDO_VERSION function replaces the SDO_ADMIN.SDO_VERSION function, which was available with the deprecated relational model of Oracle Spatial.
This section discusses some general guidelines that affect the amount of disk storage space and CPU power needed for spatial applications. They are not, however, intended to replace any other guidelines you use for general application sizing, but to supplement them.
The following characteristics of spatial applications can affect the need for storage space and CPU power:
Data volumes: The amount of storage space needed for spatial objects depends on their complexity (precision of representation and number of points for each object). For example, storing one million point objects takes less space than storing one million road segments or land parcels. Complex natural features such as coastlines, seismic fault lines, rivers, and land types can require significant storage space if they are stored at a high precision.
Query complexity: The CPU requirements for simple mapping queries, such as Select all features in this rectangle, are lower than for more complex queries, such as Find all seismic fault lines that cross this coastline.
Spatial error message numbers are in the range of 13000 to 13499. The messages are documented in Oracle9i Database Error Messages.
Oracle Spatial provides examples that you can use to reinforce your learning and to create models for coding certain operations. Several examples are provided in the following directory:
$ORACLE_HOME/md/demos/examples
The following files in that directory are helpful for applications that use the Oracle Call Interface (OCI):
readgeom.c and readgeom.h
writegeom.c and writegeom.h
This guide also includes many examples in SQL and PL/SQL. One or more examples are usually provided with the reference information for each function or procedure, and several simplified examples are provided that illustrate table and index creation, as well as several functions and procedures:
Inserting, indexing, and querying spatial data (Section 2.1)
Coordinate systems (spatial reference systems) (Section 5.8)
Linear referencing system (LRS) (Section 6.6)
|
 Copyright © 1999, 2002 Oracle Corporation All rights reserved |
|