| Type | Description | Examples |
| Discrete (Type - I) | Individual settling, low solids concentration | Grit, sand |
| Flocculant (Type - II) | Dilute suspension, particles flocculate, mass and settling rate increase with depth | Primary and upper secondary settlers |
| Hindered (Type - III) | Intermediate concentration, mass settles as a unit, interface at top | Secondary clarifiers |
| Compression (Type - IV) | High concentration, structure formed, compression causes settling | Sludge |
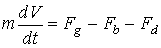
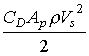



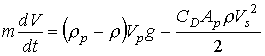
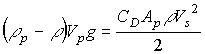
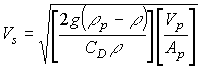
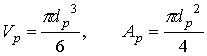


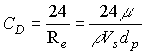
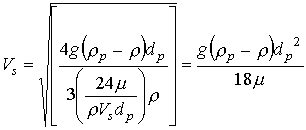
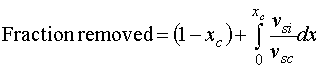
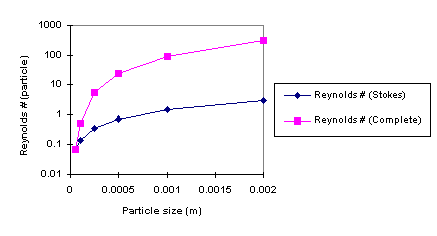
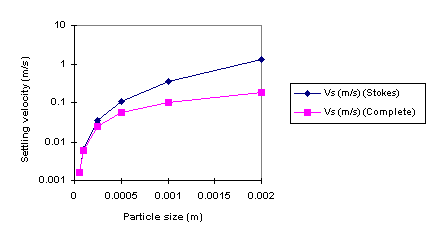



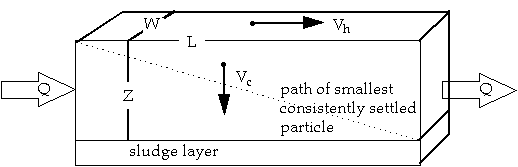
 "Longidutal Section of a Circular Sedimentation Tank"...
"Longidutal Section of a Circular Sedimentation Tank"...