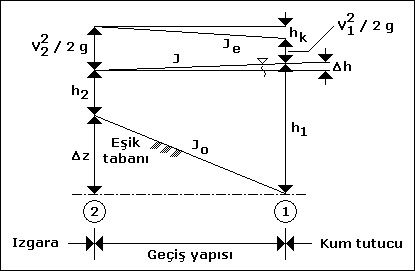
Su yüzeyi eğimi kanal taban eğiminden farklı ve kanal taban eğimi ise gerekli akım koşullarını sağlamak üzere belirli sınırlar içerisinde normalden daha eğimlidir. Bu nedenlerden dolayı, hidrolik tasarım esasları bakımından izlenecek yol üniform olmayan akım koşullarını içerir ve mansaptan menbaya doğru bir tasarım sürecini öngörür. Geçiş yapısındaki hidrolik olgu aşağıdaki şekilde verilmiştir.
Açık kanallar için " Manning " denklemi aşağıdaki gibidir ;
V O = ( 1 / n ) ( R ) 2 / 3 ( J E ) 1 / 2
Burada ; V O : ortalama yatay akım hızı ( m / sn ), R : hidrolik yarıçap ( m ), n : " Manning " pürüzlülük katsayısı ve J E : enerji çizgisi eğimi.
Enerji çizgisi eğimi aşağıdaki eşitlik ile verilmektedir ;
J E = ( h K ) / ( L G )
Burada ; h K : geçiş yapısında oluşan yük kaybı ( m ) ve L G : geçiş yapısı uzunluğu ( m ).
Yukarıdaki iki denklem birleştirilecek olursa ve ayrıca süreklilik denklemi gereği aşağıdaki eşitlik yazılabilir ;
h K = [ ( Q ) 2 ( n ) 2 ( L G ) ] / [ ( A ) 2 ( R ) 4 / 3 ]
Burada ; A : ıslak enkesit alanı ( m 2 ).
Islak enkesit alanının ve hidrolik yarıçapın değerleri olarak 1 ve 2 numaralı kesitlerdeki büyüklüklerin ortalama değerleri alınırsa, aşağıdaki eşitlikler yazılabilir ;
R O = ( R 1 + R 2 ) / 2
A O = ( A 1 + A 2 ) / 2
1 ve 2 nımaralı kesitler arasında " Bernoulli " denklemi uygulanacak olursa, aşağıdaki eşitlik elde edilebilir ;
( V 2 2 / 2 g ) + h 2 + DELTA z = ( V 1 2 / 2 g ) + h 1 + h K
Burada ; V 1 ve V 2 : sırası ile, 1 ve 2 nolu kesitlerdeki yatay akım hızları ( m / sn ), h 1 ve h 2 : sırası ile, 1 ve 2 nolu kesitlerdeki su yükseklikleri ( m ) ve DELTA z : eşik yüksekliği ( m ).
Yukarıdaki şekilden görüleceği üzere, 1 ve 2 nolu kesitlerdeki su yüzeyleri arasındaki fark, ( DELTA h ) aşağıdaki denklem ile ifade edilebilir ;
DELTA h = h 1 - h 2 - DELTA z
Yukarıdaki ilk iki denklem birleştirilecek olursa aşağıdaki eşitlik elde edilir ;
DELTA h = ( V 2 2 / 2 g ) - ( V 1 2 / 2 g ) - h K
Hesap esası bir iterasyon gerektirmekte ve DELTA h parametresinin kabul edilen ve hesaplanan değerlerine göre bir yaklaşım yapılmaktadır. Daha önce değinildiği gibi, hesap süreci içindeki akış mansaptan menbaya doğrudur. Bu nedenle ızgara kanalı taban genişliği için bir ön hesap gerekmektedir. Hidrolik tasarım süreci içerisinde ızgara çıkış kanalı taban genişliğinin saptanmasında, açık kanallar için önerilen B = 2 h eşitliği kullanılabilir. Geçiş yapısının uzunluğunun saptanmasında tedrici genişleyen yan duvarların ayrılma açıları 8 ila 9 O arasında olmalıdır. Ancak, bu kadar küçük açıların geçiş yapısının uzunluğunu arttıracağı unutulmamalıdır.
