


 |
 |

| OLASILIK |
A) Semih’in öğretmeni ilk derste olasılık konusuna giriş yapmıştı ve zarlardan , yazı tura atmaktan, bir torba içinden farklı renkteki topları çekmekten bahsetmişti. Tenefüste Semih arkadaşı ile yeni öğrendikleri konu hakkında konuşurken arkadaşı Semih’e “iki tane parayı aynı anda atarsak ikisinin de tura gelme şansı ne olur acaba?” dedi. Semih deneyelim dedi ve cebinden iki tane bozuk para çıkardı ve atmaya başladılar. Sizde olası sonuçları aşağıdaki ağaç diyagramında yerleştirip, çıkabilecek sonuçları boş bırakılan yere yazın ve bu sonuçların olasılıklarını hesaplayın. |
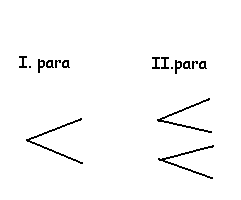 |
| Sonuçlar : .......... |
| Çıkan sonuçların olasılıkları: .......... |
| Bu sonuçları tek tek ağaç diyagramı çizmeden I ve II. Paraların fırlatılmaları sonuçlarından yararlanarak nasıl bulabileceğinizi düşünün. |
B) Bu defa Semih’in aklına bir soru geldi “derste zar ile parayı ayrı ayrı atınca sonuçlarını bulduk , peki ya ikisini beraber atmış olsaydık sonuçlar ne olurdu acaba?” Arkadaşı ağaç diyagramı yapmayı önerdi. * Aşağıdaki boşluğa ağaç diyagramını siz oluşturun. |
| Sonuçlar : .......... |
| Çıkan sonuçların olasılıkları: .......... |
| İlk basamaktaki gibi zar ve para sonuçlarından yararlanarak olasılığı bulabilmek için farklı bir yol bulmaya çalışın. |
 |
| C) İki tavla zarının aynı anda atıldığı zaman çıkabilecek olası sonuçları ağaç diyagramı kullanmadan yazmaya çalışın. |
D) İlk basamakta birinci paranın yazı gelme olasılığı a olsun, ikinci paranın da yazı gelme olasılığı b olsun : a ∆ b : ( YY gelme olasılığı) ……… a ile b hangi işleme sokulmalı ki sizin bulduğunuz sonucu versin? İlk atılan paranın tura gelme olasılığına c , ikinci paranın da tura gelme olasılığına d diyelim: c ∆ d : ( TT gelme olasılığı)………. Sıra önemli olmadığı için TY ve YT aynı şeydir. Öyle ise : (TY)……..: c ∆ b (YT)……..: a ∆ d (TY veya YT gelme olasılığı) …………:(c ∆ b) ◊ (a ∆ d) Bulduğunuz sonuçları ikinci ve üçüncü basamak için kullanın. Ağaç diyagramı ile bulduğunuz sonuçlarla bağdaştı ise bulduklarınızdan yararlanarak bir genellemeye varın. |

